2 Regimes de Juros Simples
Este capítulo apresenta os conceitos do regime de juros simples e, por meio de exemplos numéricos, mostra como se comporta o crescimento de uma aplicação sob este regime ao longo do tempo. O regime de juros simples é usado em casos específicos no mercado de capitais como em operações de curto prazo, em razão de sua facilidade de cálculo. Ele é muitas vezes empregado para diminuir ou “inflar” artificialmente a taxa de juros compostas. A partir disso, algumas instituição financeira se utilizam desse fato para realizar publicidade de produtos financeiros ao público leigo.
Na medida em que avançamos no curso, vamos introduzindo as nomeclaturas utilizadas na literatura. Neste capítulo também vamos começar a operar com a calculadora financeira Hp12c, como forma alternativa para facilitar os cálculos. Ela possui a vantagem de ter diversas fórmulas financeiras programadas, o que não são encontradas normalmente em outras calculadoras. Todavia, como dito no preâmbulo do livro, sinta-se a vontade para buscar o recurso que melhor se ajuste as suas necessidades.
A calculadora Hp12c possui a seguinte diagramação do seu teclado. A primeira operação que vamos realizar é ajustar o número de casas decimais. Para isso digite as seguintes teclas f 9. Observe que o número de casas decimais irá aumentar. Toda vez que realizar os cálculos nos exemplos ou nos exercícios sempre confira o número de casas decimais. Caso não esteja adequado realize esse procedimento.
Como vimos no capítulo anterior, com o passar do tempo esperamos que seja acrescida uma determinada quantia positiva ao agente que abriu mão da sua preferência temporal de consumo. Demos uma interpretação a este valor ao qual referenciamos de juros. A partir disso, podemos conceituar-lo da seguinte maneira.
Note que este conceito não empõe a maneira como é gerado a quantia do juros. Transcorrido o tempo em que o agente cedeu sua preferência temporal o acréscimo do juros lhe confere um novo valor ao qual chamamos de montante.
A partir dos conceitos apresentados estabelecemos a seguinte relação:
\[ \text{montante} = \text{principal} + \text{juros}. \tag{2.1}\]
Em princípio são possíveis diversas formas de se computar o valor do juros que gera a diferença entre o montante e o principal. Uma maneira de avaliar o valor do juros seria registrar um determinado percentual do valor do principal no instante inicial e ir acrescentando este valor para cada período que for sendo transcorrido. A este método de calcular denominamos de regime simples de juros.
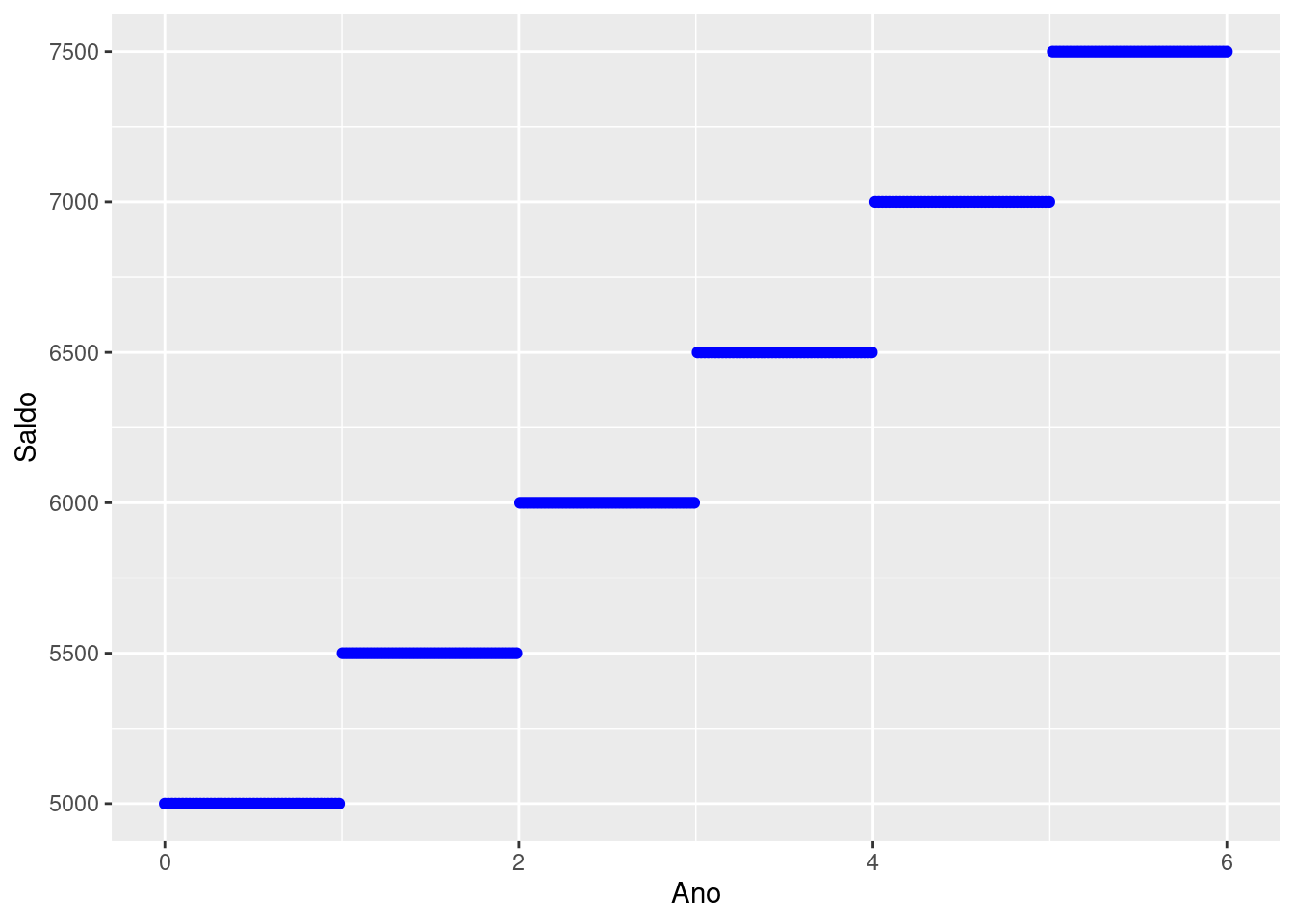
Exemplo 2.1 (Banco ACME) O investidor Pinky deseja aplicar R$ 5.000,00 no banco ACME com uma taxa de juros de 10% a.a. O banco ACME adota o regime de juros simples para seus correntistas e investidores. Transcorridos 5 anos, contabilize qual saldo credor que o Pinky terá no banco ACME ao final de cada ano.
| Ano | Valor Base | Saldo Início Ano | Juros Ano | Saldo Final Ano | Proporção |
|---|---|---|---|---|---|
| 1 | 5000 | 5000 | 500 | 5500 | 0.1000 |
| 2 | 5000 | 5500 | 500 | 6000 | 0.0909 |
| 3 | 5000 | 6000 | 500 | 6500 | 0.0833 |
| 4 | 5000 | 6500 | 500 | 7000 | 0.0769 |
| 5 | 5000 | 7000 | 500 | 7500 | 0.0714 |
Ao final de cada ano o valor referente ao juros é de R$ 500. A proporção, como já havíamos visto, decresce ao longo do tempo. A função que descreve o crescimento do investimento, \(\psi_{0.1}(n,5000)\), é uma função linear.
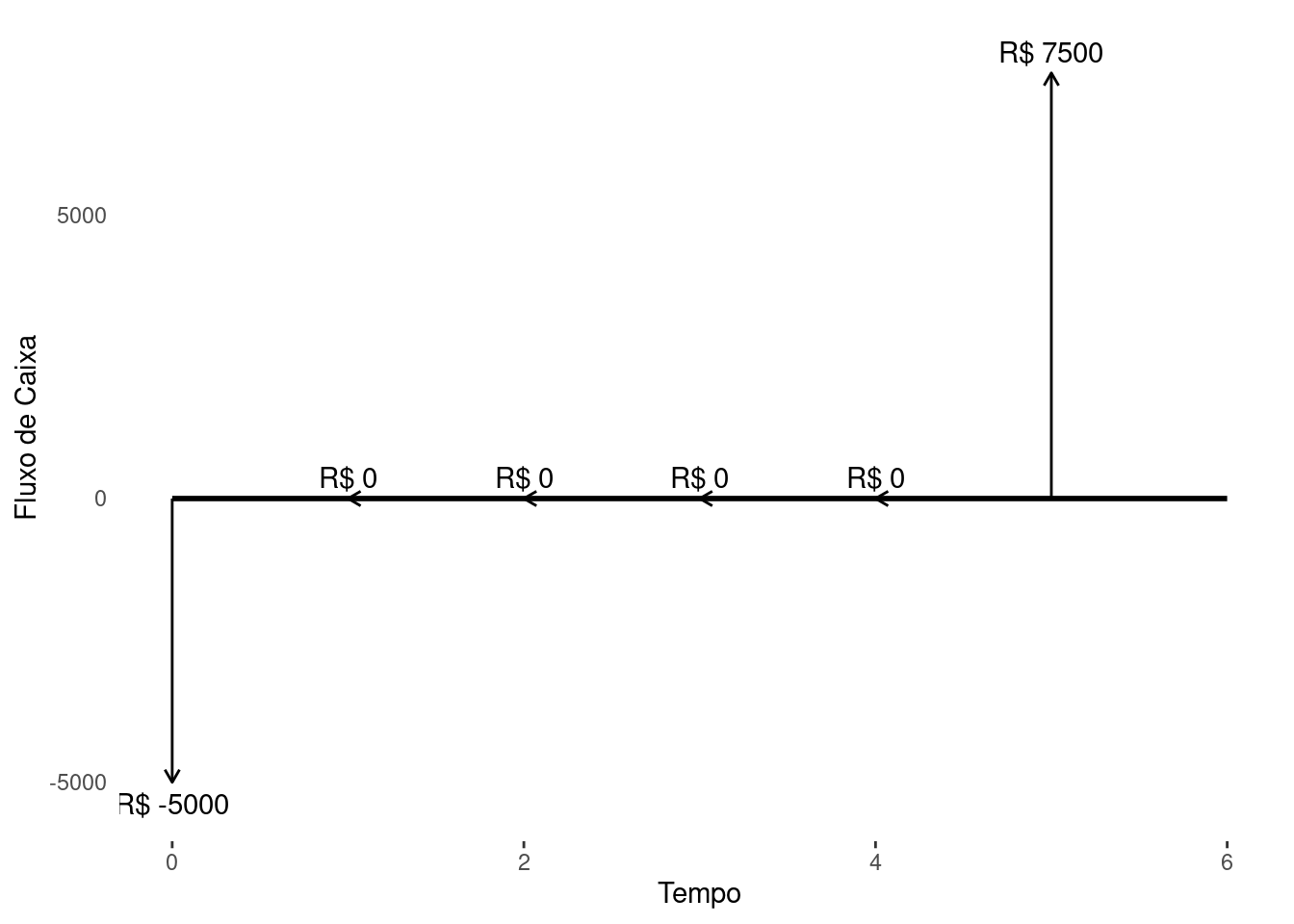
O diagrama de fluxo de caixa que representa a operação do Pinky é descrito abaixo. Observe que há apenas duas movimentações. A primeira ocorre no momento em que ele faz o depósito para fazer o investimento e a segunda e última movimentação no momento em que faz o resgate da aplicação.
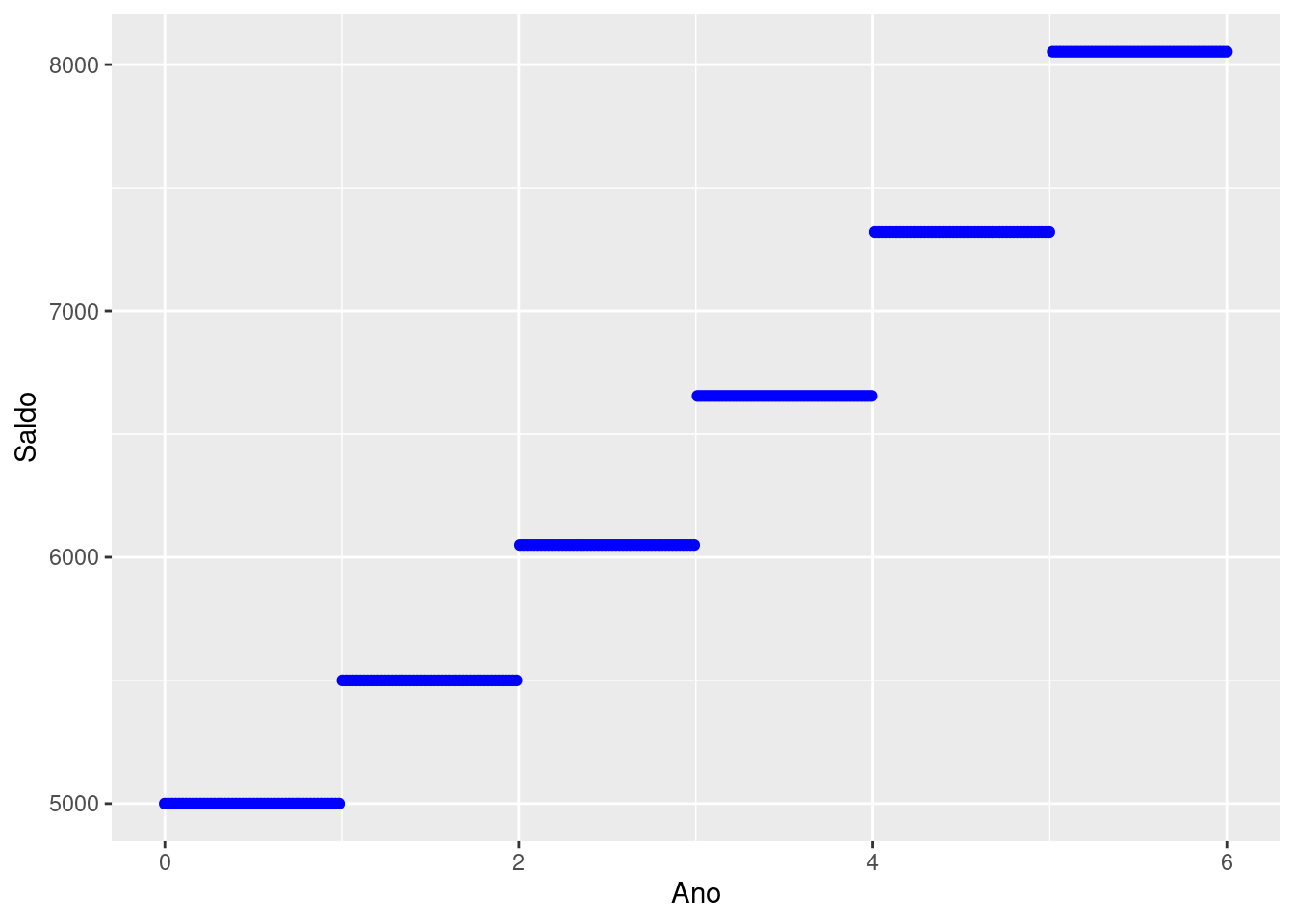
Pensando nisso, um outro investidor chamado Cérebro decide também aplicar seus recursos neste banco. No entanto, ele deseja fazer de uma maneira um pouco diferente de Pinky. Cérebro retira todo saldo no final de cada ano e aplica novamente no início do ano seguinte.
| Ano | Valor Base | Saldo Início Ano | Juros Ano | Saldo Final Ano | Proporção |
|---|---|---|---|---|---|
| 1 | 5000 | 5000 | 500 | 5500 | 0.1000 |
| 2 | 5500 | 5500 | 550 | 6050 | 0.1000 |
| 3 | 6050 | 6050 | 605 | 6655 | 0.1000 |
| 4 | 6655 | 6655 | 665 | 7320 | 0.0999 |
| 5 | 7320 | 7320 | 732 | 8052 | 0.1000 |
Perceba que o simples fato do Cérebro retirar no final do ano e aplicar novamente no início do ano subsequente muda o resultado. Isto ocorre porque a cada momento que ele faz a aplicação a base para o cálculo do juros muda. Desta maneira, todo começo de ano se torna um novo valor inicial do investimento.
Claramente o resultado da estratégia do Cérebro se mostrou diferente da adotada por Pinky. Sendo o mesmo banco e o mesmo produto financeiro para ambos os irmão, por que essa diferença ocorre?
Na literatura, quando utilizamos a função \(\psi_i(n,V_{0})\) para projetar seu valor no futuro denotamos por \(FV\). Como vimos, o juros ganhos no regime simples são obtidos sobre o principal, fazendo com que os juros tenham o mesmo valor em todos os períodos. Desta forma, o montante de juros de cada período é \(PV\cdot i\) em que \(i\) é a taxa de juros do período. Sendo \(n\) a quantidade de períodos, então o montante total de juros obtido é \(PV\cdot i\cdot n\). Portanto, o valor \(FV\) é constituído por meio da Equação 2.1 quando por ele é remunerado via regime simples.
\[ \begin{align} \text{FV} & = \text{PV}+n\cdot\text{PV}\cdot{i} \\ & = PV\cdot(1+i\cdot n). \end{align} \tag{2.2}\]
Caso a variável de interesse seja o \(PV\), então basta reescrever a Equação 2.2.
\[ PV = \frac{FV}{1+i\cdot n}. \tag{2.3}\]
O período de referência da taxa de juros aplicada \(i\) deve coincidir com a referência de tempo empregada para designar o número de períodos \(n\).
Cabe ressaltar que os juros chamado de exatos são aqueles que levam em consideração o calendário do ano civil, ou seja, 365 dias. Já os juros ditos comerciais são aqueles que levam em consideração o ano comercial com 360 dias sendo 30 dias por mês. Os juros exatos pouco são usados nos tradicionais financiamentos comerciais. A mecânica com a qual operamos sobre o valor presente ou o valor futuro são se altera. Apenas temos que ficar atentos a estas definições sobre a marcação da linha do tempo para não incorremos em inconsistência de valores. Mesmo na hipótese de se utilizar a relação entre as variáveis de maneira correta as inconsistências vão aparecer. Sua significância vai depender de caso a caso. Como estamos mais preocupados em compreendermos a mecânica de operação e as interpretações entre as variáveis a luz de um problema geral, não daremos muita ênfase nesta distinções, salvo quando expresso. Contudo, na vida cotidiana é importante que o leitor saiba da existência desses calendários.
2.1 Desconto Por Dentro ou Racional
A taxa de juros \(i\), denominada como taxa de rentabilidade ou também taxa de desconto por dentro, pode ser obtida a partir da Equação 2.2.
\[ i = \frac{1}{n}\left(\frac{FV}{PV}-1\right). \tag{2.4}\]
O montante do desconto, expresso em valores monetários, corresponde aos juros acumulados ao longo dos períodos. Em outras palavras, ele coincide com a diferença entre o valor futuro \(FV\) e o principal \(PV\). \[ D_{in} = FV - PV. \]
Nos casos práticos, o valor do \(PV\) é desconhecido ao passo que as variáveis \(FV\), prazo, dado em números de períodos \(n\), e a taxa de desconto \(i\) são conhecidas. Substituindo \(PV\) na equação acima pela Equação 2.3 temos
\[ \begin{align} D_{in} & = FV-\frac{FV}{1+i\cdot n}\\ & = \frac{FV(1+i\cdot n)-FV}{1+i\cdot n}\\ & = FV\cdot\frac{i\cdot n}{1+i\cdot n}. \end{align} \]
Alternativamente, o valor de desconto por dentro \(D_{in}\) pode ser calculado realizando o produto do valor do principal, taxa de rentabilidade e o número de períodos.
\[ D_{in} = PV\cdot i\cdot n. \]
Exemplo 2.2 (Resgate de Título via Hp12c) Calcule o valor da taxa mensal de desconto por dentro usada numa operação de desconto de 60 dias de um título cujo valor de resgate é R$10.000,00 e cujo valor do principal é R$9.750,00
Sendo um total de 60 dias para encontrarmos a taxa mensal precisamos definir quantidade de período equivalente a esse período. Considerando o mês com 30 dias então 60/30 equivale a \(n=2\) meses. Utilizando a Equação 2.4 encontramos o valor de \(i\). \[ i = \frac{1}{n}\left(\frac{FV}{PV}-1\right)=\frac{1}{2}\left(\frac{10.000}{9.750}-1\right)=0,01282. \] Portanto encontramos a taxa de desconto por dentro de 1,282%.
Para realizar estes cálculos por meio da calculadora financeira Hp12c basta realizar os seguintes procedimentos.
Pressione as teclas
10ENTER9.75÷o que resulta em \(1,026=10.000/9,750\) e memórias\(X\leftarrow 1.025641\)
\(Y\leftarrow 9.75\)
\(Z\leftarrow 10\)
Pressione as teclas
1-o que resulta em \(0,025641=1,025641-1\) e memórias\(X\leftarrow 0.025641\)
\(Y\leftarrow 1\)
\(Z\leftarrow 1.025641\)
\(T\leftarrow 9.75\)
Pressione as teclas
0.5xo que o que resulta em \(0,01282=0.5\cdot 0,025641\) e memórias\(X\leftarrow 0.01282\)
\(Y\leftarrow 0.5\)
\(Z\leftarrow 0.025641\)
\(T\leftarrow 1\)
Lembre dos registros da memória da Hp12c \((X, Y, Z, T)\).
2.2 Desconto Por Fora, Comercial ou Bancário
O desconto dito por fora ou comercial é obtido pela aplicação da taxa de desconto \(j\) sobre o valor futuro \(FV\). O valor do desconto comercial, \(D_{out}\) é obtido realizando o produto do valor futuro \(FV\), da taxa de desconto \(j\) por período e do número de períodos de desconto \(n\). \[ D_{out} = FV\cdot j \cdot n. \] O valor presente \(PV\), ou principal, resultante do desconto por fora durante \(n\) períodos com uma taxa de desconto bancária \(j\) por período é expresso no regime de juros simples por
\[ \begin{align} PV & = \text{montante final}-\text{desconto}\\ & = FV-FV\cdot n\cdot j\\ & = FV\cdot(1- n \cdot j). \end{align} \tag{2.5}\]
Salienta-se que na Equação 2.5 há uma limitação nos valores de \(n\) e \(j\) de maneira que o produto dessas variáveis devem respeitar a restrição \(n j<1\). Caso contrário o valor encontrado pode ser negativo. Reescrevendo a Equação 2.5 é possível explicitar a expressão do valor do desconto bancário
\[ j = \frac{1}{n}\left(1-\frac{PV}{FV}\right). \]
Repare que a taxa de desconto por fora é aplicado sobre \(FV\) para se obter \(PV\), enquanto que a taxa de desconto por dentro ou taxa de rentabilidade \(i\) é aplicada sobre \(PV\) para se obter \(FV\). O valor total do desconto em ambos os casos refere-se a diferença entre \(PV\) e \(FV\)
A partir da Equação 2.3 e Equação 2.5 podemos estabelecer uma relação entre os descontos por dentro e por fora. Para isto basta igualarmos ambas as equações.
\[ \begin{align} \frac{FV}{1+in}& = FV(1-dn)\\ jn & = 1-\frac{1}{1+in}\\ j&=\frac{i}{1+in}. \end{align} \tag{2.6}\]
O valor total do desconto em ambos os casos (por dentro e por fora) refere-se a diferença entre \(PV\) e \(FV\). Para obter tal diferença aplica-se uma taxa de desconto distintas (\(i\) e \(j\)) sobre um determinado valor (\(PV\) e \(FV\)) por um determinado tempo (\(n\)). Intuitivamente podemos deduzir que para manter a mesma diferença entre \(PV\) e \(FV\) a taxa \(j\) deve ser menor do que \(i\) visto que o valor de \(FV\) é maior do que \(PV\). A conclusão de que \(j\leq i\) também pode ser facilmente verificada através da Equação 2.6. Seguindo a mesma equação obtém-se a expressão da taxa de desconto por dentro \(i\) em razão da taxa de desconto bancária \(j\).
\[ i = \frac{j}{1-jn}. \]
Nas operações bancárias de desconto de títulos, usualmente empregam-se o conceito de taxa de desconto por fora, normalmente denominada apenas por taxa de desconto (por quê?).
Exemplo 2.3 (Desconto Bancário) A pedido do seu pai, Ramonzito leva os seguintes títulos da empresa para serem descontados no banco ACME.
| Vencimentos (dias) | Valor do Título |
|---|---|
| 30 | R$ 10.000,00 |
| 60 | R$ 20.000,00 |
| 90 | R$ 30.000,00 |
| Total | R$ 60.000,00 |
Calcule o valor a ser creditado na conta da empresa, onde a taxa de desconto por mês é de 1%.
Para encontrarmos a cifra do título a valor presente \(PV\) basta utilizar a Equação 2.5 com o valor de \(j=0,01\) dado no enunciado.
- Vencimento 30 dias
\[ PV_{30} = FV(1-jn)=10.000(1-0,01\cdot 1) = 9.900. \] - Vencimento 60 dias
\[ PV_{60} = FV(1-jn)=20.000(1-0,01\cdot 2) = 19.600. \] - Vencimento 90 dias
\[ PV_{90} = FV(1-jn)=30.000(1-0,01\cdot 3) = 29.100. \]
Deste modo, o valor creditado deverá ser
\[
PV = PV_{30}+PV_{60}+PV_{90} = 9.900 + 19.600 + 29.100= 58.600.
\]
Do total de R$ 60.000,00 distribuídos em três meses de entrada, o valor equivalente para recebimento imediato na conta da empresa é de R$ 58.600,00.
2.3 Exercícios
Exercício 2.1 Um investidor aplicou R$1.000,00 numa instituição financeira que remunera seus depósitos a uma taxa de 5% ao trimestre, no regime de juros simples. Mostre o crescimento desse capital no final de cada trimestre, a contar da data da aplicação dos recursos, e informe o montante que poderá ser retirado pelo investidor no final do 6º trimestre, após a efetivação do último depósito.
Exercício 2.2 Uma instituição financeira oferece a seus clientes uma taxa de rentabilidade de 1,2% ao mês, a juros simples. Calcule o valor da renda (\(FV-PV\)) de uma aplicação de R$10.000,00 efetuada nessa instituição, por um prazo de 18 dias.
Exercício 2.3 Um empresário tem uma conta de cheque especial num banco que permite saques a descoberto e que cobra 1,5% ao mês sobre o saldo devedor, a juros simples, pelos dias que a conta ficar descoberta. Calcule o montante de juros cobrado no mês de abril, assumindo que a conta tem saldo zero no final de março e que em abril são emitidos os seguintes cheques:
| Data | Valor do Cheque |
|---|---|
| 1º de abril | 2.000,00 |
| 11 de abril | 1.000,00 |
| 21 de abril | 1.000,00 |
Exercício 2.4 Um título com 39 dias a decorrer está sendo negociado com uma rentabilidade de 1,20% a.m. Assuma o ano comercial e calcule a taxa anual de desconto por fora que corresponde à essa taxa de rentabilidade.
