1 Introdução
Neste capítulo abordamos brevemente os principais conceitos e fundamentos que norteiam a matemática financeira. Inicialmente, para melhor localizar o leitor, são apresentadas resumidamente as principais demonstrações contábeis, dentre elas a de fluxo de caixa (DFC). Por meio de diagrama vamos construir uma representação esquemática do fluxo de caixa juntamente com suas convenções e simbologias. Na sequência, introduzimos a ideia do valor do dinheiro no tempo, e como corolário a existência do juros. Por fim, desenvolveremos as ideias básicas da capitalização de um ativo e o comportamento de seu valor ao longo do tempo.
1.1 Matemática Financeira
O campo da matemática financeira, em essência, trata-se da análise do valor do dinheiro ao longo do tempo. O seu estudo é composto por um conjunto de equações para modelar as principais variáveis econômicas e relacionar os valores de uma quantia no tempo presente bem como o seu valor equivalente no futuro. As ferramentas desenvolvidas pela matemática financeira trazem a vantagem de nortear os tomadores de decisão em suas análises econômica-financeiras de modo a tornar a abordagem com maior acurácia e objetividade (Dal Zot e Castro 2015).
1.2 Demonstração Contábil
As demonstrações contábeis são relatórios estruturados da situação patrimonial, financeira e das transações realizadas em um determinado intervalo de tempo por uma entidade. A obrigação da construção das demonstrações para fins legais dependem da sua natureza jurídica.
O objetivo das demonstrações vão muito além da obrigação legal. Elas são úteis para fornecer informações para uma ampla variedade de usuários na tomada de decisões. Há um elemento estratégico na construção de demonstrações contábeis, pois permitem obter uma visão gerencial da empresa bem como desenvolver métricas para análise de performance e eficiência das operações da empresa tais como: rentabilidade do ativo (return on asset - ROA), rentabilidade de patrimônio líquido (return on equity - ROE), EBITDA, giro de estoque, alavancagem financeira, alavancagem operacional etc. Outro ponto importante é sua desejável integração com outros métodos de gestão estratégicas como o Balanced Scorecard (BSC) ou mesmo a realização análise comparativa de eficiência entre unidades da própria empresa ou concorrência como o método Data Envelopment Analysis (DEA). As principais demonstrações são: Balanço Patrimonial (BP), Demonstração do Resultado do Exercício (DRE) e Demonstração do Fluxo de Caixa (DFC).
1.2.1 Balanço Patrimonial
O balanço patrimonial tem o objetivo de descrever os recursos da empresa. Seu valor é resultado do fluxo de caixa onde cada recurso tem uma origem e uma destino. Desta forma, a construção do patrimônio da empresa é constituído através de uma relação de igualdade entre ativo e passivo.
Ativo: São os bens, direitos e valores que a empresa possui e podem ser convertidos em benefícios econômicos futuros.
Passivo: São as obrigações e dívidas da empresa, ou seja, as contas a pagar e outras responsabilidades financeiras.
O balanço patrimonial tem a seguinte estrutura
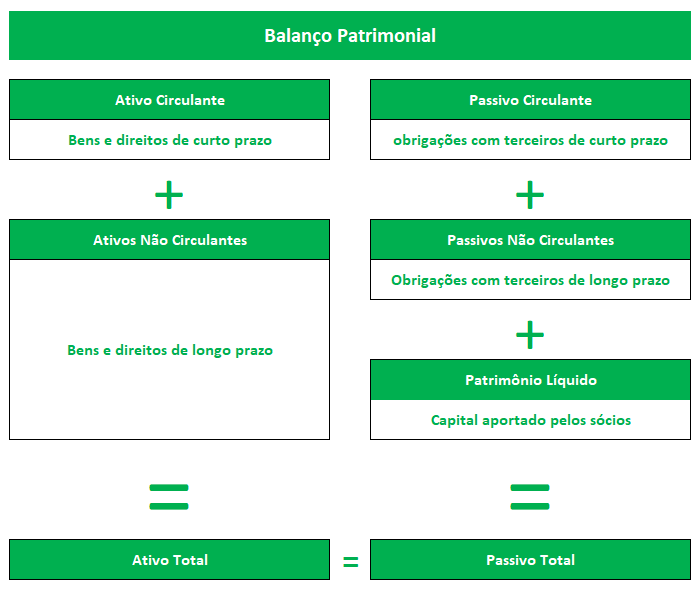
O demonstrativo do lado esquerdo (balanço patrimonial ativo) descreve todos os bens e direitos que uma empresa possui contabilizado, podendo o mesmo ser dividido em duas partes:
Ativos circulantes: todos os ativos da empresa que deverão ser gastos, consumidos ou vendidos dentro de um período de 12 meses.
Ativos não circulantes: ativos de permanência duradoura na empresa, comumente relacionados com o funcionamento da mesma e que normalmente não espera-se que sejam gastos, consumidos ou vendidos dentro do prazo de 12 meses.
Por outro lado, os recursos financiados destes ativos são descritos pelo (balanço patrimonial passivo) localizado no lado direito do BP sendo dividido em dois grupos:
Capital de Terceiros: composto por dívidas no mercado financeiro que as empresas emitem para financiar as suas atividades operacionais (debêntures) ou mesmo empréstimos bancários.
Capital Próprio: montante total de recurso na empresa que tem como proprietários os sócios/acionistas da empresa.
Desta forma, podemos descrever essa relação de igualdade através da seguinte equação:
\[ \text{Ativo} = \text{Passivo}+\text{Patrimônio Líquido.} \]
Segue abaixo um exemplo de balanço patrimonial da empresa de calçados Arezzo. Como esperado note que o valor do ativo total é igual ao passivo total.
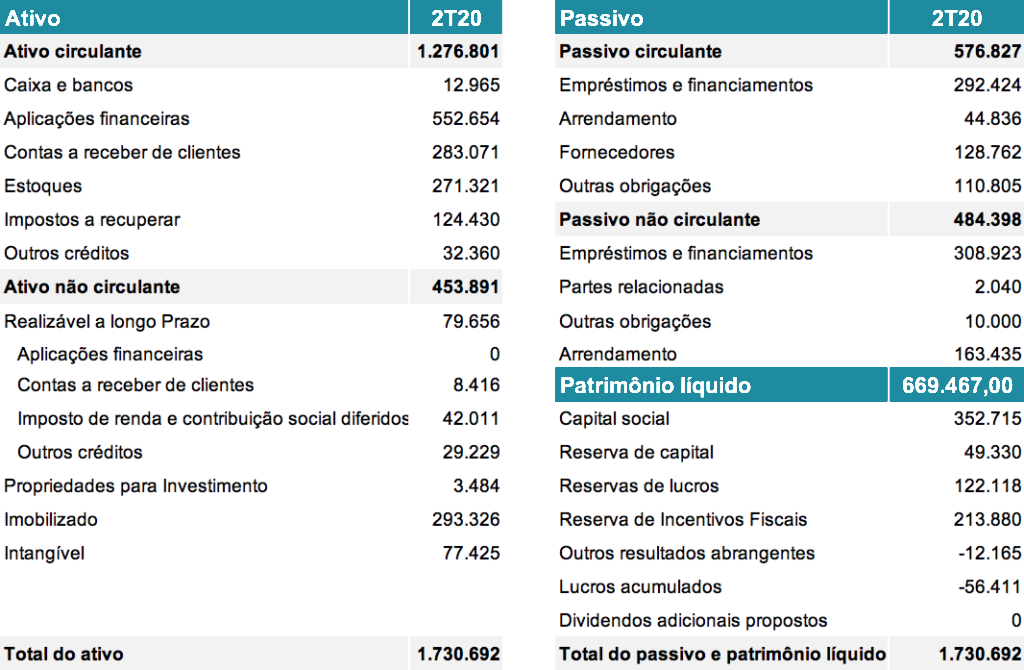
1.2.2 Demonstração do Resultado do Exercício
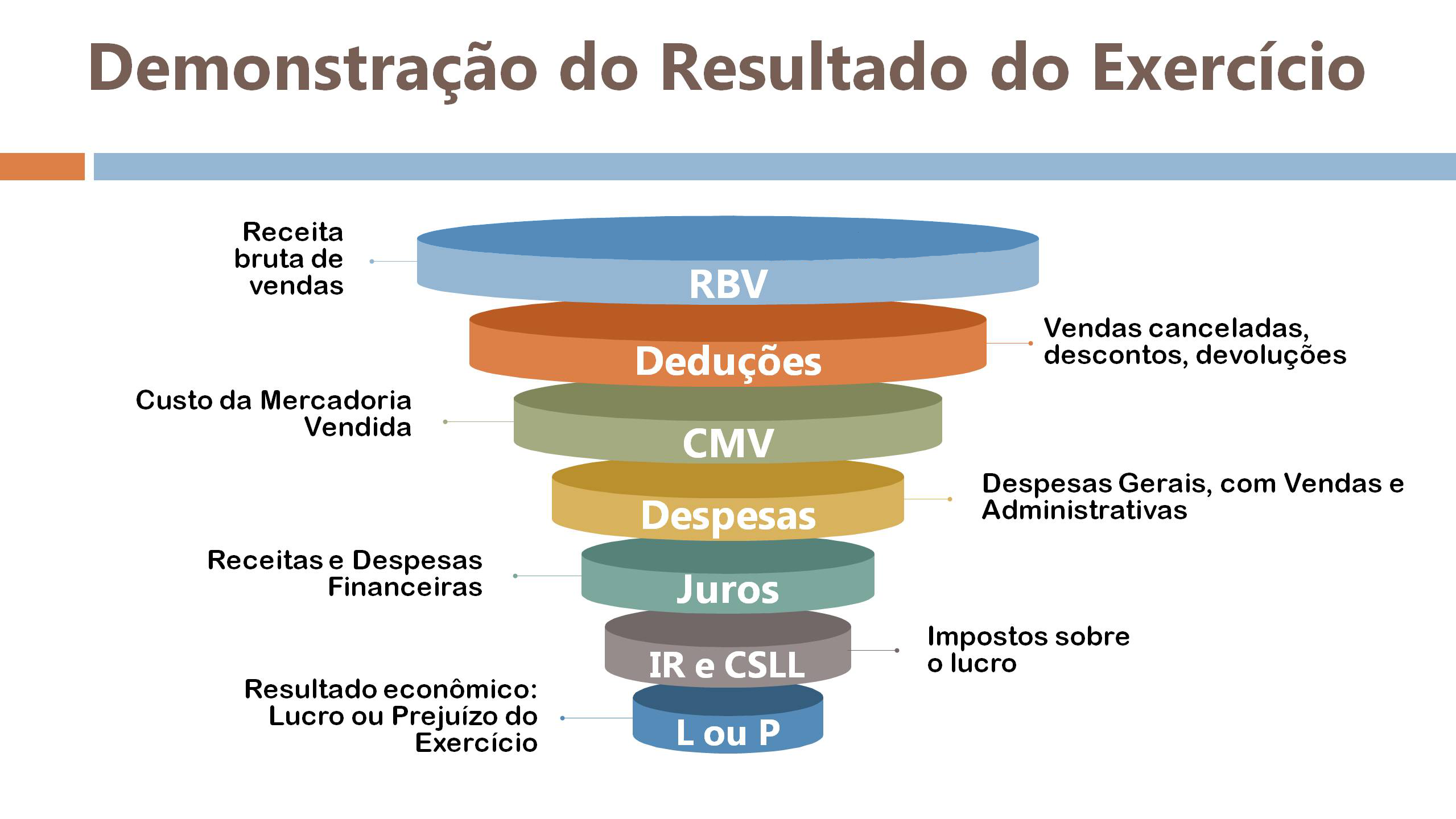
Um dos relatórios mais utilizados na análise gerencial e também contábil é a demonstração do resultado do exercício (DRE) e tem por objetivo apresentar como a empresa atingiu seu resultado. Na DRE são contabilizadas todas as receitas e todas as despesas. A performance é evidenciada tanto em caso de lucro como de prejuízo incorridas em um determinado período de tempo.
Tanto as receitas quanto as despesas são computadas mediante a realização do seu fato gerador. Portanto, as receitas e despesas ocorrem independente da entrada ou saída de recursos do caixa. Em outras palavras, a apuração da DRE é feita a partir do regime de competência ou econômico (princípio competência), o que contrasta com o regime de caixa.
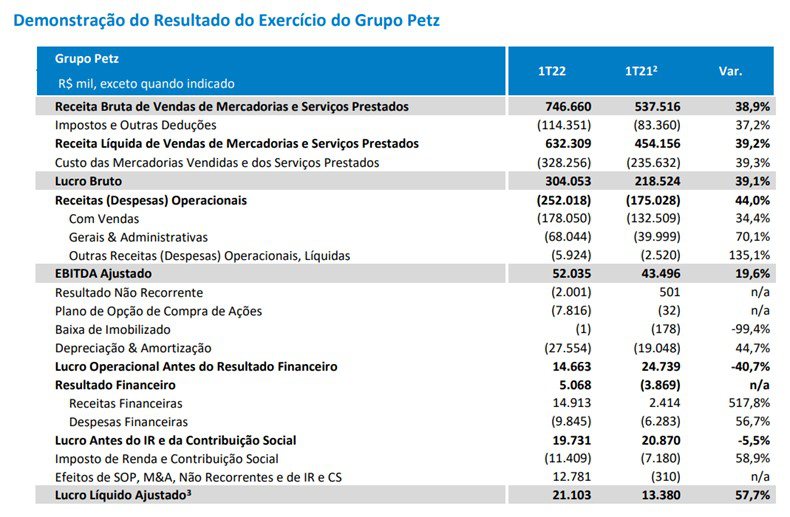
Abaixo segue um exemplo de demonstrativo do resultado do exercício (DRE) do grupo Petz para o primeiro trimestre de 2022.
1.2.3 Demonstração do Fluxo de Caixa
Denomina-se fluxo de caixa o conjunto de entradas e saídas de recursos, com liquidez imediata, ao longo do tempo. A apreciação do fluxo de caixa pode envolver tanto movimento financeiro de uma empresa quanto de um fundo de investimentos, na gestão de projetos, operações financeiras, comerciais ou mesmo pessoais.
A elaboração e análise do fluxo de caixa é indispensável em diversas atividades empresariais sobretudo no estudo de viabilidade econômico-financeira de projetos de investimentos. No contexto corporativo, o relatório responsável por evidenciar as movimentações ocorridas no caixa da empresa, ou equivalente de caixa ocorridos um determinado período de tempo é o demonstrativo de fluxo de caixa (DFC). Essas movimentações podem ser decorrentes de atividades operacionais, de investimento ou de financiamento da empresa.
Devido sua natureza, o regime contábil adotado é o regime de caixa, diferentemente do DRE. A partir do DFC computa-se as entradas e saídas de caixa da empresa evidenciando objetivamente a origem dos recursos. Dessa maneira, a DFC não estabelece nenhuma vinculação entre um superávit financeiro a um eventual lucro, no mesmo período de avaliação. Por esta mesma razão, uma empresa pode apresentar entradas volumosas de recursos em caixa concomitantemente com a realização de prejuízos em suas atividades operacionais.
A demonstração do fluxo de caixa pode ser dividido em 3 seções:
Atividades Operacionais
Atividades de Investimento
Atividades de Financiamento
O montante de caixa recebido ou gasto em cada uma das seções é adicionada ao final para calcular o volume total de caixa movimentado pela empresa. Abaixo segue um exemplo de demonstração do fluxo de caixa.
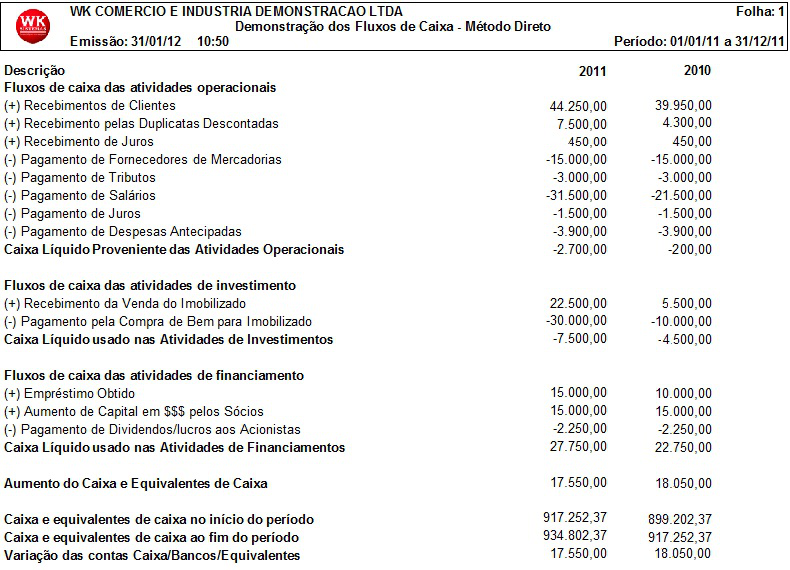
A partir das características das demonstrações contábeis tratadas anteriormente, podemos destacar as diferenças entre DRE e DFC. A figura abaixo evidencia de forma sintética essas diferenças.
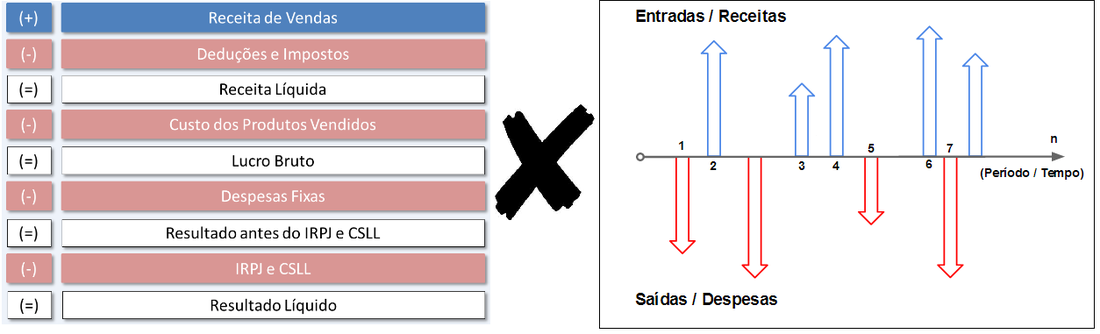
1.3 Diagrama de Fluxo de Caixa
A descrição das movimentações de entrada e saída de recursos do caixa que não tenham fins contábeis ou fiscais pode ser feita de diversas formas. A representação esquemática do fluxo de caixa mais usual é feita por meio do diagrama de fluxo de caixa.
O diagrama de fluxo de caixa adota as seguintes convenções:
A reta horizontal representa o tempo, dividido em períodos regulares e discretos.
Os intervalos de tempo são todos iguais.
Os valores monetários são referentes ao final do período. Isto é, a capitalização é realizada de forma descontínua.
As saídas de caixa são representadas com sinais negativos (-) e são indicadas com setas para baixo.
As entradas de caixa são representas com sinais positivos (+) e são indicadas com setas para cima.
Dependendo do caso, empregamos as setas como saldo do fluxo de caixa. Deste modo, fica configurada no máximo uma seta por período. Outra forma é explicitar diversos fluxos ocorridos de maneira que teremos várias setas para cada período. O conjunto das setas, representando os saldos do fluxo é geralmente chamado de série de pagamentos.
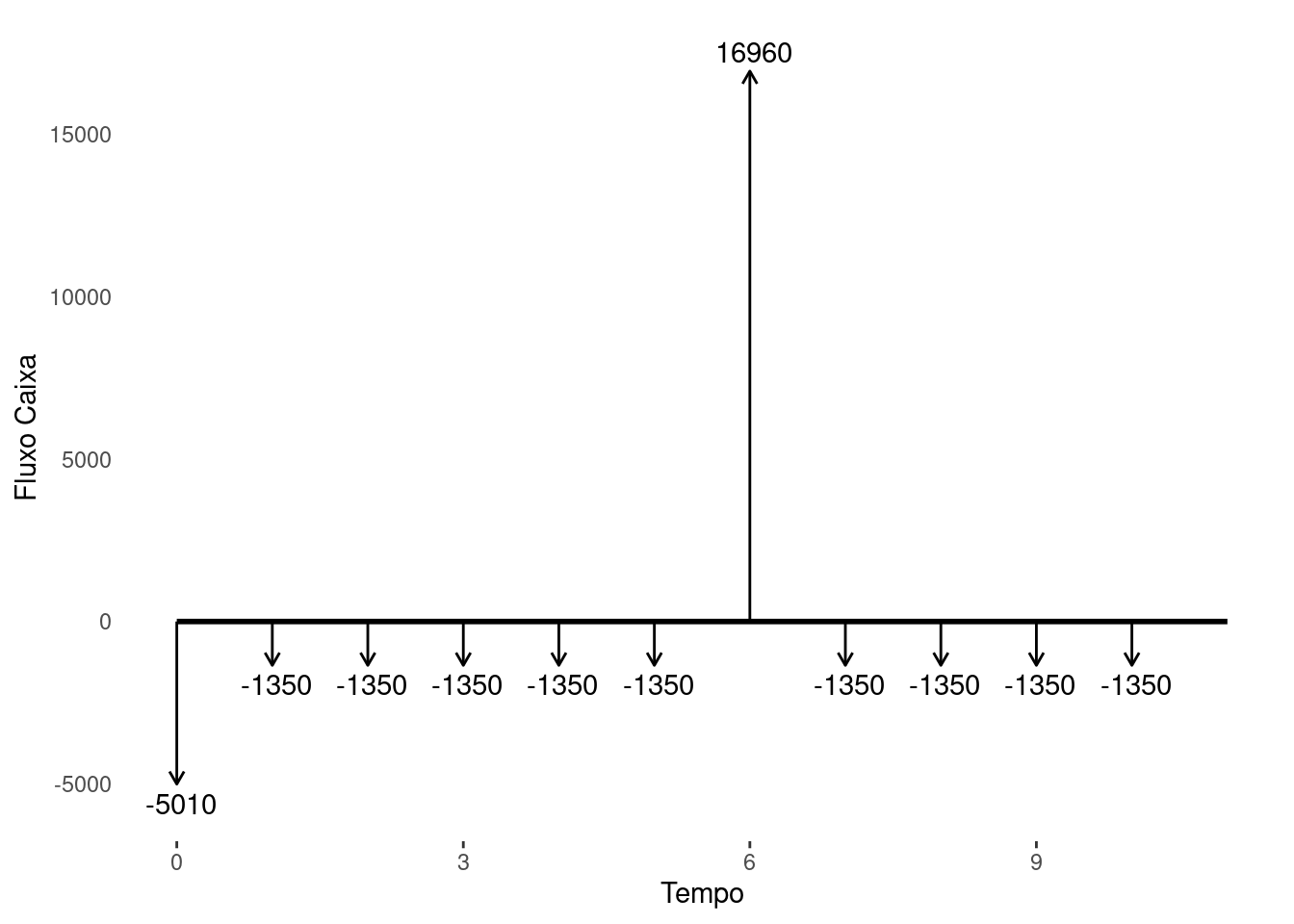
Exemplo 1.1 (Exemplo Fluxo de Caixa) Rubinho comprou seu carro em 10 parcelas de R$ 1.350,00 e uma entrada de R$ 5.010,00. Na 6ª parcela, ele vende seu carro para seu amigo Michael por R$ 18.310,00. Monte o diagrama de fluxo de caixa do Rubinho para esta operação.
1.4 Juros
Uma interpretação cotidiana do juros dentro das práticas de mercado pode ser estabelecida como a remuneração do capital empregado em atividade produtiva, ou a remuneração paga/cobrada por instituição financeira sobre o capital nela aplicado/tomado. Em uma visão mais ampla, os juros podem ser entendidos como o valor de aluguel do recurso moeda dentro de uma economia.
Os juros são fixados por meio de taxas, normalmente descrito em percentual. O valor da taxa é expresso conjuntamente com o período de tempo ao qual os juros são aplicados. O período é simbolizado pela sigla “a.” mais a sigla da unidade de tempo. Para representar o ano, semestre, mês, dia são utilizados as seguintes letras respectivamente: “a”, “s”, “m” e “d”. A título de exemplo, para escrever dois porcento de juros aplicado ao mês teríamos 2% a.m. e para escrever onze porcento de juros aplicado ao ano seria 11% a.a.
1.5 Moeda
Ativo financeiro de aceitação geral utilizado na troca de bens e serviços que tem o poder liberatório (capacidade de pagamento) instantânea. Sua aceitação é garantida por lei. Ela tem curso “forçado” e sua única garantia é a legal.
A moeda dentro de uma economia deve cumprir pelo menos três funções, a saber:
Meio ou instrumento de troca
Unidade de medida ou unidade de conta
Reserva de valor
A moeda representa um direito sobre as mercadorias de uma economia. Ela pode ser guardada para uso posterior, visto que serve como reserva de valor ou forma de poupança. Note que a moeda serve de reserva de valor para um determinado agente, mas não para toda a sociedade. O que determina a riqueza de uma economia é a sua capacidade de produção global e não o montante de moeda existente.
Inicialmente vamos considerar a hipótese de uma moeda estável. Posteriormente, vamos trabalhar com o caso de moedas com instabilidade geral nos níveis de preço. Entretanto, vale destacar que os conceitos da matemática financeira são integralmente aplicáveis em ambos os casos.
1.6 Valor do Dinheiro no Tempo
A maioria das pessoas intuitivamente possui a noção de que R$ 100,00 hoje não são equivalentes aos mesmos R$ 100,00 daqui a um ano. Essa percepção é ainda mais forte, visto que observamos isso empiricamente. Todavia, para compreendermos melhor esse fenômeno, sem apelar meramente à intuição, podemos construir a partir de alguns pressupostos simples e raciocínio lógico um argumento em favor desta percepção.
Para analisarmos o valor do dinheiro no tempo, considere que podemos mensurar através de uma função matemática a sensação ou sentimento de “satisfação” de um agente econômico com o consumo de uma certa quantidade \(x\) do bem \(A\) no tempo \(t\). Essa função é chamada de função utilidade. Por meio dela, descrevemos o comportamento de suas preferências de consumo. Isto posto, suponha por hipótese, que as preferências dos agentes econômicos têm as seguintes propriedades:
Os agentes sempre buscam maximizar sua função utilidade. Portanto, se um agente pode escolher um entre dois produtos ou bens distintos, digamos \(A\) e \(B\), ele irá escolher \(A\) em detrimento de \(B\) sempre que \(u_{A}(x,t)>u_{B}(x,t)\) e será indiferente entre \(A\) e \(B\) sempre que \(u_{A}(x,t)=u_{B}(x,t)\).
O agente sempre prefere consumir ou possuir um bem qualquer \(A\) no presente momento do que este mesmo bem em uma data futura. Em outras palavras, temos que \(u_{A}(x,t+\epsilon )<u_{A}(x,t)\) onde \(\epsilon>0\) (Preferência Temporal).
Para uma dada quantidade \(x>0\) do bem \(A\) o agente sempre prefere por quantidades adicionais \(c>0\) deste bem. Em outros termos tem-se que \(u_{A}(x,t) < u_{A}(x+c,t)\). Esta propriedade é invariante no tempo.
Sem perda de generalidade, vamos considerar que o preço de cada item do bem \(A\) é de \(p_{A}\) e permanece constante ao longo de tempo. O agente possui no instante \(t\) um montante de \(M_t=p_{A}\cdot x\). Pela Propriedade 1, a quantidade \(y\) do bem \(A\) no tempo \(t+\epsilon\) necessária para que o agente fique indiferente entre receber \(x\) unidades de \(A\) no tempo \(t\) deve ser a solução da Equação 1.1.
\[ u_{A}(y, t+\epsilon) = u_{A}(x, t). \tag{1.1}\]
Entenda a solução da equação como o valor de \(y\) tal que a equação acima seja satisfeita. Pela Propriedade 2, se \(y=x\) então
\[ u_{A}(x, t+\epsilon) < u_{A}(x, t). \]
Desta forma, a quantidade do bem \(A\) no tempo \(t+\epsilon\) não pode ser a mesma no tempo \(t\), uma vez que não satisfaz a Equação 1.1. Pela Propriedade 3, para \(\delta>0\) temos
\[ u_{A}(x, t+\epsilon) < u_{A}(x+\delta, t+\epsilon). \tag{1.2}\]
Caso exista um \(y\) que satisfaça a Equação 1.1, ele deve ser estritamente maior do que \(x\). Novamente pela Propriedade 2, este valor deve ser crescente com relação a \(\delta^{*}_{\epsilon}\). Assim,
\[ u_{A}(x+\delta^{*}_{\epsilon}, t+\epsilon) = u_{A}(x, t) \Leftrightarrow y = x + \delta^{*}_{\epsilon}. \tag{1.3}\]
Assim, pela Equação 1.3, para que um agente fique indiferente entre receber \(x\) unidades do bem \(A\) no tempo \(t\) e receber em um momento posterior, \(t+\epsilon\), ele deve ser recompensado com \(\delta^{*}_{\epsilon}\) unidades a mais. Computando o valor das unidades adicionais \(m=p_{A}\cdot\delta^{*}_{\epsilon}\), encontramos o montante de juros \(m\), que o agente recebe por abrir mão do valor de \(M_{t}\) por um período \(\epsilon\). A taxa de juros obtida no período \(\epsilon\) é calculada por
\[ r_{t}=\frac{1}{M_{t}}\frac{M_{t+\epsilon}-M_{t}}{\epsilon}=\frac{1}{\epsilon}\left(\frac{M_{t+\epsilon}}{M_{t}}-1\right). \]
Em condições normais a taxa de juros praticada no mercado deve refletir o equilíbrio entre todos os agentes integrantes desse mercado. A introdução de alguns agentes sem preferência temporal numa economia, isto é, agentes que possuem função utilidade com a propriedade \(u(x,t)=u(x,t+\epsilon)\) desloca o ponto de equilíbrio para um novo ponto ótimo no sentido de Pareto. Os agentes com preferências temporais drenam todo o orçamento dos agentes sem preferência temporal para aumentar sua utilidade com consumo imediato ou por meio de empréstimo a outros agentes acrescidos de juros. Como a fonte do recurso não incide juros, então essa diferença é adicionada ao seu orçamento. Por consequência, sua utilidade é maximizada sem prejuízos a ninguém. Mesmo em uma situação hipotética, agentes sem preferência temporal geram comportamentos anômalos aos quais esperamos em observações empíricas.
A dinâmica dos agentes econômicos acerca de suas preferências e restrições orçamentárias são objetos de estudo da área de economia chamada de microeconomia. Portanto, um melhor entendimento do comportamento dos agentes exigem maiores conhecimentos desta área, o que está fora do escopo deste curso. Um material introdutório altamente recomendado em microeconomia é o Varian (2006).
Uma consequência imediata dos pressupostos supracitados com respeita a função utilidade é que a noção intuitiva do valor do dinheiro no tempo, discutida no início da seção, é um fenômeno natural e esperado numa economia. Apesar do desenvolvimento dos argumentos acima fundamentarem na microeconomia, a matemática financeira adota a relação do valor do dinheiro no tempo de forma axiomática. Para nossos propósitos é suficiente assumir que esta relação é verdadeira. Entretanto, é desejável que o leitor compreenda a sua fundamentação teórica e suas implicações nas observações empíricas do valor do dinheiro no tempo.
O ótimo de Pareto numa economia ocorre quando não é possível melhorar a situação de nenhum dos agentes sem que piore a situação de um outro agente. Mais detalhes em (Varian 2006).
Neste sentido, a matemática financeira opera com cálculos envolvendo fluxo de caixa, com a correta aplicação de taxa de juros, para se levar em conta o valor do dinheiro no tempo. Assim sendo, os valores financeiros são grandezas que só podem ser comparados e operados algebricamente quando a data de referência é a mesma. Para dois ativos distintos \(V_{t}\) e \(V'_{t}\), e a partir da função que descreve a evolução do valor do ativo dada por
\[ V_{t} = \psi_{r}(t,V_{0}), \] onde \(V_{0}\) é o valor inicial do ativo \(V_{t}\) e \(r\) a taxa de juros, estamos aptos a realizar comparações entre seus valores, uma vez que podemos mensurar \(V_{t}\) qualquer instante de tempo. Tomando a data de referência \(t=q\), então computamos \(V'_{q}\) e \(\psi_{r}(q,V_{0})\) para podermos operar com os valores desses ativos. Abaixo segue um exemplo da evolução do valor de um ativo que é governado pela função \(\psi_{r}(t, V_{0})\).
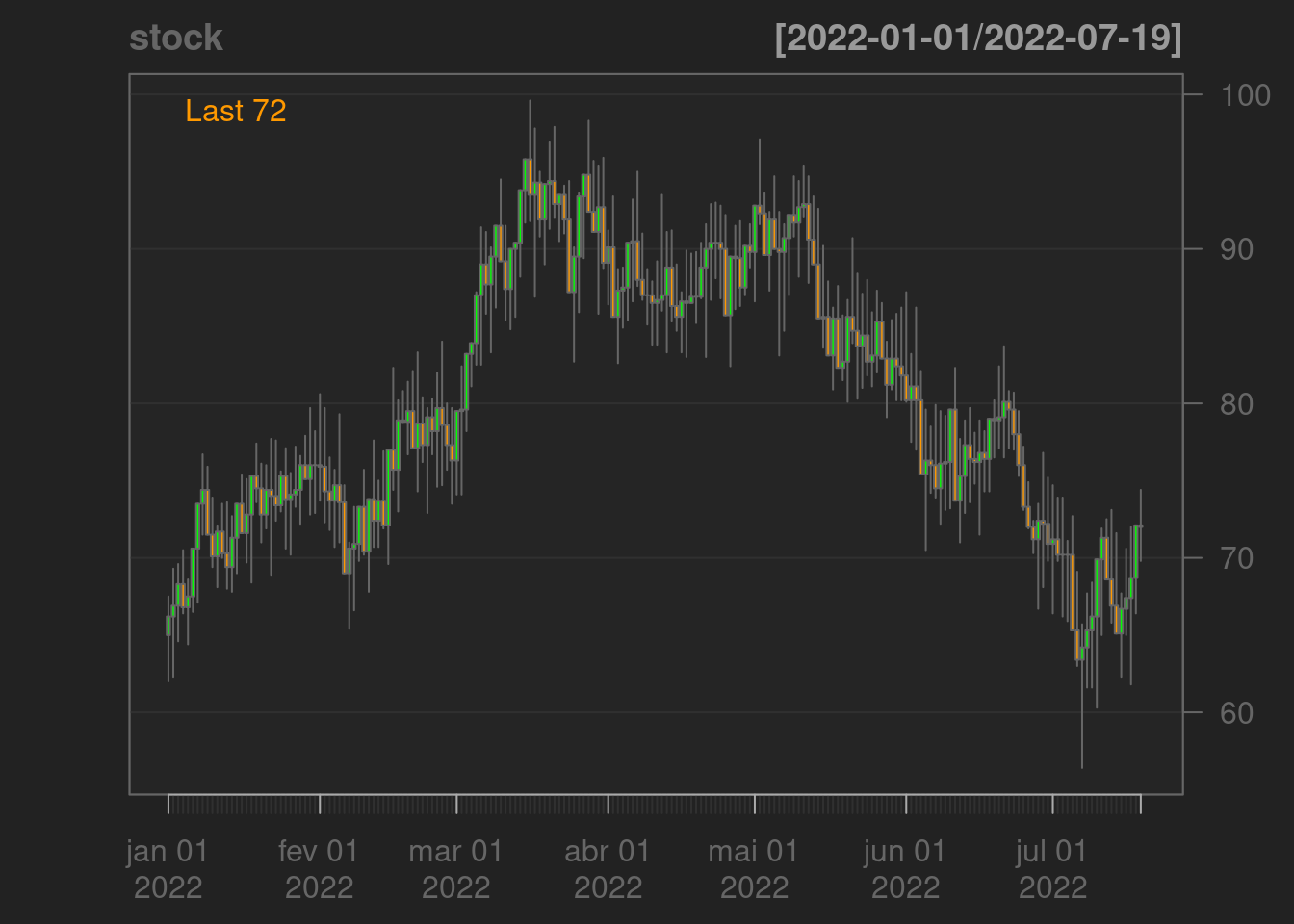
1.7 Capitalização
Mediante ao regime no qual um determinado ativo remunera o investidor, é possível obter uma expressão fechada para \(\psi_{r}(t,V_{0})\). A partir disso, conseguimos apontar seu valor em qualquer momento. Levando em conta o período no qual o ativo remunera ou muda de valor, temos basicamente duas formas de capitalização, a capitalização contínua e a capitalização discreta. Denomina-se capitalização de juros o ato de adicionar juros ao capital.
Na capitalização contínua, a cada fração infinitesimal de tempo o ativo remunera o investidor, isto é, o ativo a todo instante muda seu valor. Para tal, descrevemos a remuneração de um ativo por meio de sua derivada \(\frac{dV_{t}}{dt}\) com relação ao tempo. O símbolo \(d\) representa um acréscimo \(\epsilon\) muito pequeno, tão pequeno quanto desejarmos, de maneira que avaliamos a razão da mudança ocorrida no valor de um ativo entre o instante de tempo \(t\) e \(t+\epsilon\) pelo intervalo \(\epsilon\) de tempo.
Na capitalização discreta, a remuneração ocorre em um conjunto contável de tempo. Em outros termos, o valor do ativo permanece constante durante todo seu período de capitalização, e recebe sua remuneração somente no momento final de cada um deles. Boa parte dos investimentos chamados de renda fixa, a capitalização é feita de forma discreta. Computamos a remuneração ocorrida para cada período de capitalização do ativo por \(\frac{\Delta V_{t}}{\Delta t}\), onde \(\Delta\) representa uma diferença de períodos \(\Delta V_{t} = V_{t+1} - V_{t}\). Os intervalos de tempo \(\Delta t\) normalmente designam os mesmos intervalos com o qual o ativo é capitalizado.
Na seção de capitalização contínua será empregado um pouco de cálculo diferencial e integral. Caso o leitor não tenha nenhuma familiaridade com esta disciplina, então poderá pular direto para a seção referente a capitalização discreta.
1.7.1 Capitalização Contínua
Uma situação comum nos mercados financeiros são de ativos que sua taxa de mudança são proporcionais ao montante acumulado. Isso ocorre de tal sorte que o valor adicionado a cada intervalo de tempo infinitesimal será tanto maior quanto maior for o valor do ativo \(V_{t}\). Este comportamento é descrito pela Equação 1.4.
\[ \frac{d}{dt}V_{t} \propto V_{t}. \tag{1.4}\]
O símbolo \(\propto\) designa o sinal de proporcionalidade. Isso significa que a menos de uma constante, ambos os lados da equação são iguais. Exemplo: o valor \(p\) cobrado no posto de combustível é proporcional a quantidade abastecida \(l\), isto é, \(p \propto l\). No exemplo, a constante de proporcionalidade \(k\) é o preço do combustível. Logo, \(p = k\cdot l\).
Neste caso, adicionando a constante de proporcionalidade \(a>0\) temos que
\[ \frac{d}{dt}V_{t} = aV_{t} \Leftrightarrow \frac{d}{dt}\log V_{t} = a. \tag{1.5}\]
A Equação Diferencial (1.5) é facilmente resolvida integrando ambos os lados da equação.
\[ \begin{align} \log V_{t} - \log V_{0}& = at+C,\\ V_{t} & = V_{0}e^{at+C}. \end{align} \tag{1.6}\]
Como o valor inicial é \(V_{0}\), então a constante \(C=0\). Portanto, a função que descreve o movimento do valor do ativo é dada pela Equação 1.7.
\[ \psi_{a}(t,V_{0})= V_{0}e^{at}. \tag{1.7}\]
Note que o parâmetro \(a\) representa a taxa de juros (instantânea) paga pelo ativo \(V_{t}\).
O gráfico abaixo exibe a evolução do ativo (azul), de acordo com a Função 1.7, e também a razão da remuneração pelo seu valor contemporâneo, \(\frac{dV_{t}}{V_{t}dt}\) (laranja), em que \(a=0.02\) e \(V_{0}=500\).
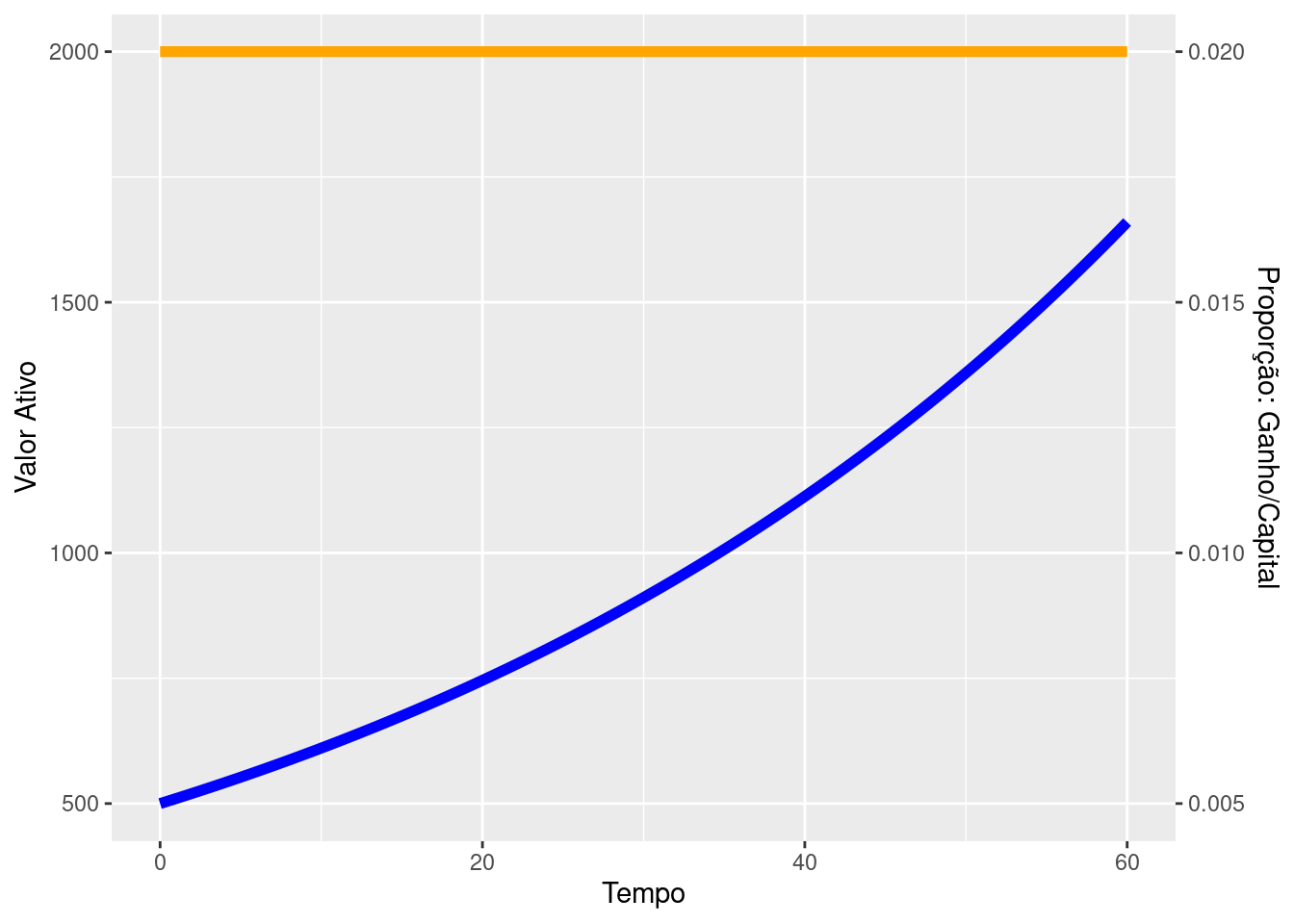
Como esperado, o valor do ativo cresce exponencialmente. Perceba que a proporção da remuneração é constante ao longo de todo tempo.
Uma situação semelhante é pensarmos em um ativo no qual sua remuneração é paga de forma proporcional ao montante inicial investido apenas.
\[ \frac{d}{dt}V_{t} \propto V_{0} \Leftrightarrow \frac{d}{dt}V_{t} = aV_{0}. \tag{1.8}\]
Considerando a constante de proporcionalidade \(a>0\) e integrando ambos os lados da Equação 1.8 obtemos
\[ V_{t} = V_{0}at+C. \tag{1.9}\]
A condição no tempo \(t=0\) define o valor inicial do ativo em \(V_{0}\), logo a constante \(C=V_{0}\). Assim, a função que descreve o comportamento desse ativo ao longo do tempo é dada por
\[ \psi_{a}(t,V_{0})= V_{0}\cdot(1+at). \tag{1.10}\]
O gráfico abaixo plota a função descrita na Equação 1.10 (azul) e a curva da razão entre a remuneração e o valor do ativo (laranja) para \(a=0.02\) e \(V_{0}=500\).
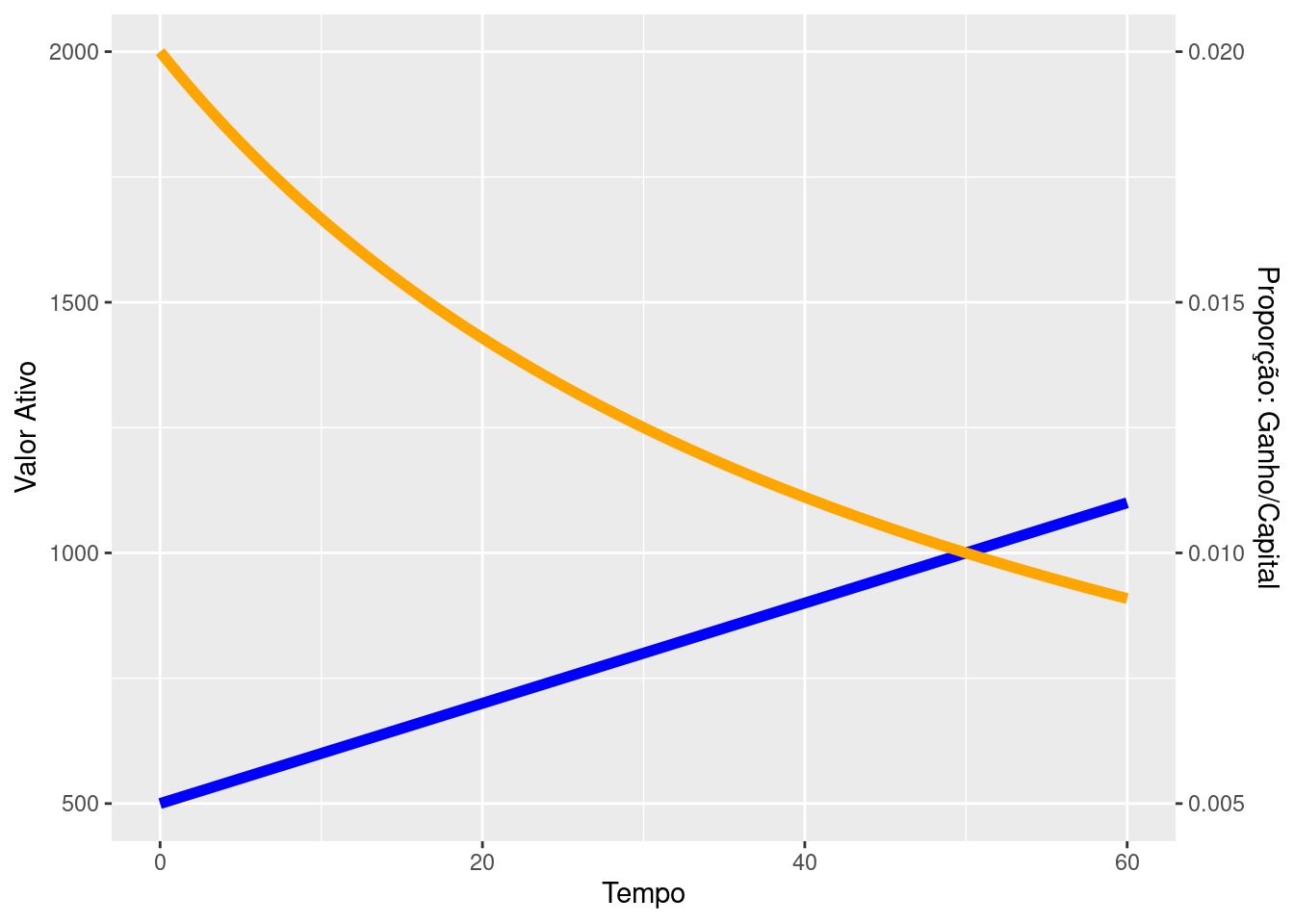
Nesta circunstância o valor do ativo cresce linearmente e a proporção da remuneração obtida pelo valor do ativo decai ao longo do tempo. Perceba que este comportamento contrasta com a situação anterior onde a remuneração é paga proporcionalmente ao valor atual do ativo e não pelo valor inicial. Enquanto naquele caso a proporção da remuneração era constante, neste caso a remuneração não acompanha a valorização do ativo.
1.7.2 Capitalização Discreta
Boa parte dos produtos financeiros oferecem remuneração proporcional ao seu valor atual. No entanto, sua capitalização ocorre de maneira discreta. Sendo assim, somente ao final de cada período ocorre a capitalização e é incorporado ao ativo sua remuneração ou juros. Um caso clássico no mercado brasileiro é da caderneta de poupança, onde a capitalização ocorre em períodos mensais e sua remuneração será tanto maior quanto o volume financeiro total acumulado. A Equação 1.11 descreve essa característica de modo similar ao caso contínuo, porém agora o valor do ativo é indexado por um tempo discreto, \(t\in \mathbb{N}\).
\[ \frac{\Delta}{\Delta t}V_{t} \propto V_{t}. \tag{1.11}\]
Adicionando uma constante de proporcionalidade
\[ \begin{align} \Delta V_{t} & = aV_{t}\Delta t. \end{align} \tag{1.12}\]
Somando ambos os lados da equação acima e sendo \(\delta=\Delta t\) uma constante temos
\[ \begin{align} \sum_{t=0}^{n} \Delta V_{t} & = \sum_{t=0}^{n} a V_{t}\delta,\\ V_{n}-V_{0} & = a\delta\sum_{t=0}^{n}V_{t}.\\ \end{align} \tag{1.13}\]
Pela Equação 1.12 podemos obter a seguinte relação de recorrência
\[ \begin{align} V_{t} & = V_{t-1}(1+a\delta),\\ & = \underbrace{V_{t-2}(1+a\delta)}_{V_{t-1}} (1+a\delta) = V_{t-2}(1+a\delta)^2,\\ &\,\, \vdots \\ & = \underbrace{V_{t-k}(1+a\delta)}_{V_{t-k+1}}\left[(1+a\delta)\cdots (1+a\delta)\right] = \cdots = V_{t-k}(1+a\delta)^k, \\ & = V_{0}(1+a\delta)^t, \end{align} \]
onde \(k\in \mathbb{N}\) e \(k\leq t\). Substituindo essa relação de recorrência na Equação 1.13 chega-se a seguinte expressão
\[ V_{n} = V_{0}\left(1 + a\delta\cdot\sum_{t=0}^{n}(1+a\delta)^{t}\right). \tag{1.14}\] Perceba que a soma na Equação 1.14 é equivalente a soma de uma PG (Progressão Geométrica). Desta maneira, utilizando-se da fórmula da soma de PG e definindo \(i=a\delta\) como o valor da taxa de juros então após algumas manipulações algébricas obtemos a expressão para \(\psi_{i}(n,V_{0})=V_{n}\) descrito na Equação Equação 1.15.
\[ \begin{align} \psi_{i}(n,V_{0}) & = V_{0}(1+i)^{n}, \,\,\,\, \text{onde } n= 0,1,2... \end{align} \tag{1.15}\]
O gráfico abaixo plota a função descrita na Equação 1.15 em azul sendo o valor \(i=0.02\) a taxa de juros e \(V_{0}=500\) o valor aplicado inicialmente.
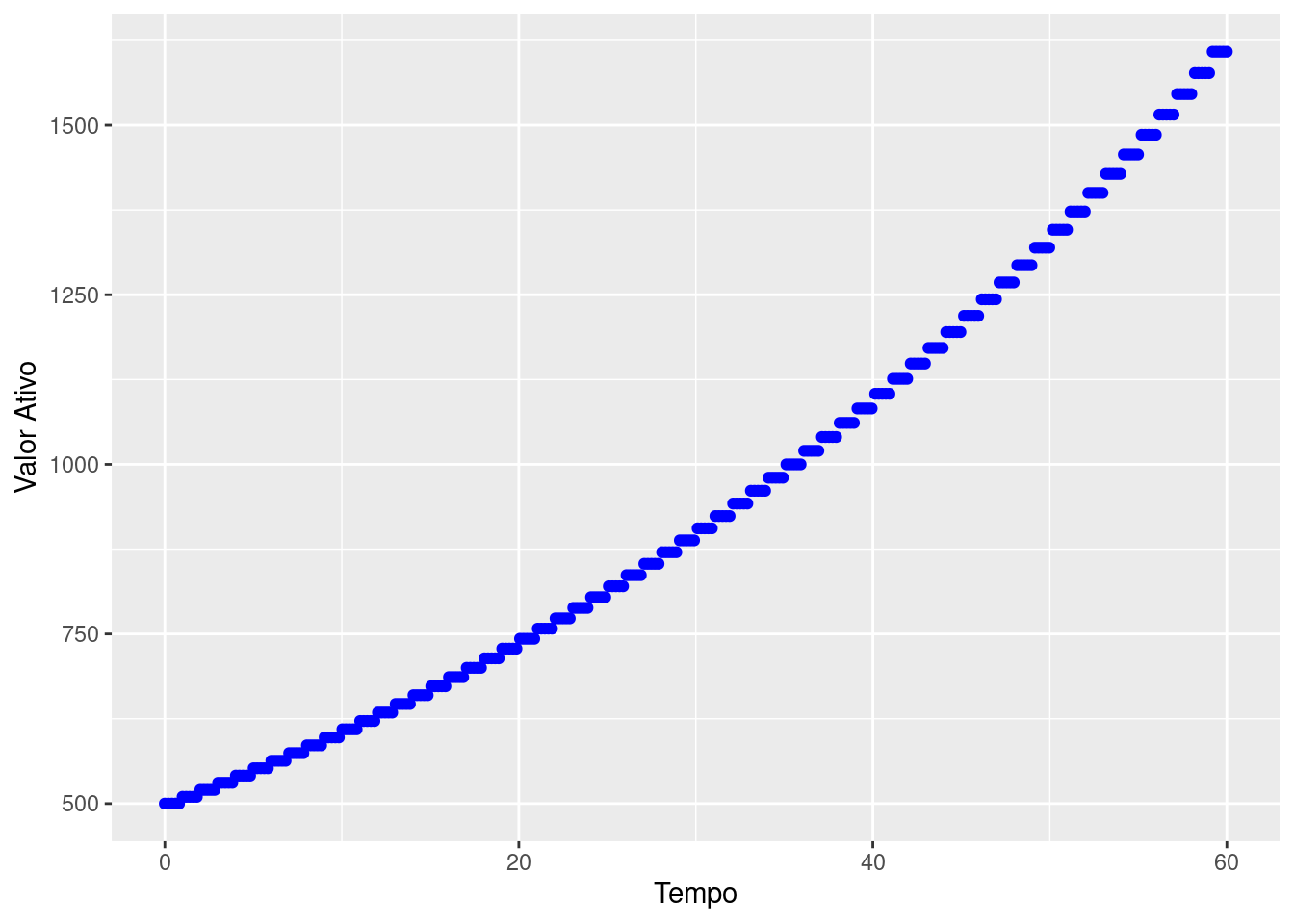
Como esperado, o valor do ativo permanece constante até o momento de sua remuneração. Repare que essa curva possui um comportamento exponencial e é muito próxima do gráfico da Figura 1.1 quando o ativo é capitalizado continuamente.
Um caso similar a este é considerar que o ativo possui uma remuneração somente proporcional ao valor aplicado no instante zero, isto é, \(\Delta V_{t}/\Delta t \propto V_{0}\). Logo, temos que
\[ \begin{align} \Delta V_{t} & = aV_{0}\Delta t. \end{align} \tag{1.16}\]
Sendo \(\delta = \Delta t\) uma constante, somando ambos os lados da Equação 1.16 e isolando \(V_{n}\) obtemos a Equação 1.17.
\[ \begin{align} V_{n} & = V_{0}(1+a\delta n). \end{align} \tag{1.17}\]
Novamente, definindo \(i=a\delta\) como o valor da taxa de juros com período de capitalização igual a \(\delta\), então temos por fim a expressão
\[ \psi_{i}(n,V_{0}) = V_{0}(1+in) \,\,\,\, \text{onde } n = 0,1,2... \]
O gráfico abaixo plota a função descrita na Equação 1.17 em azul sendo \(i=0.02\) e \(V_{0}=500\).
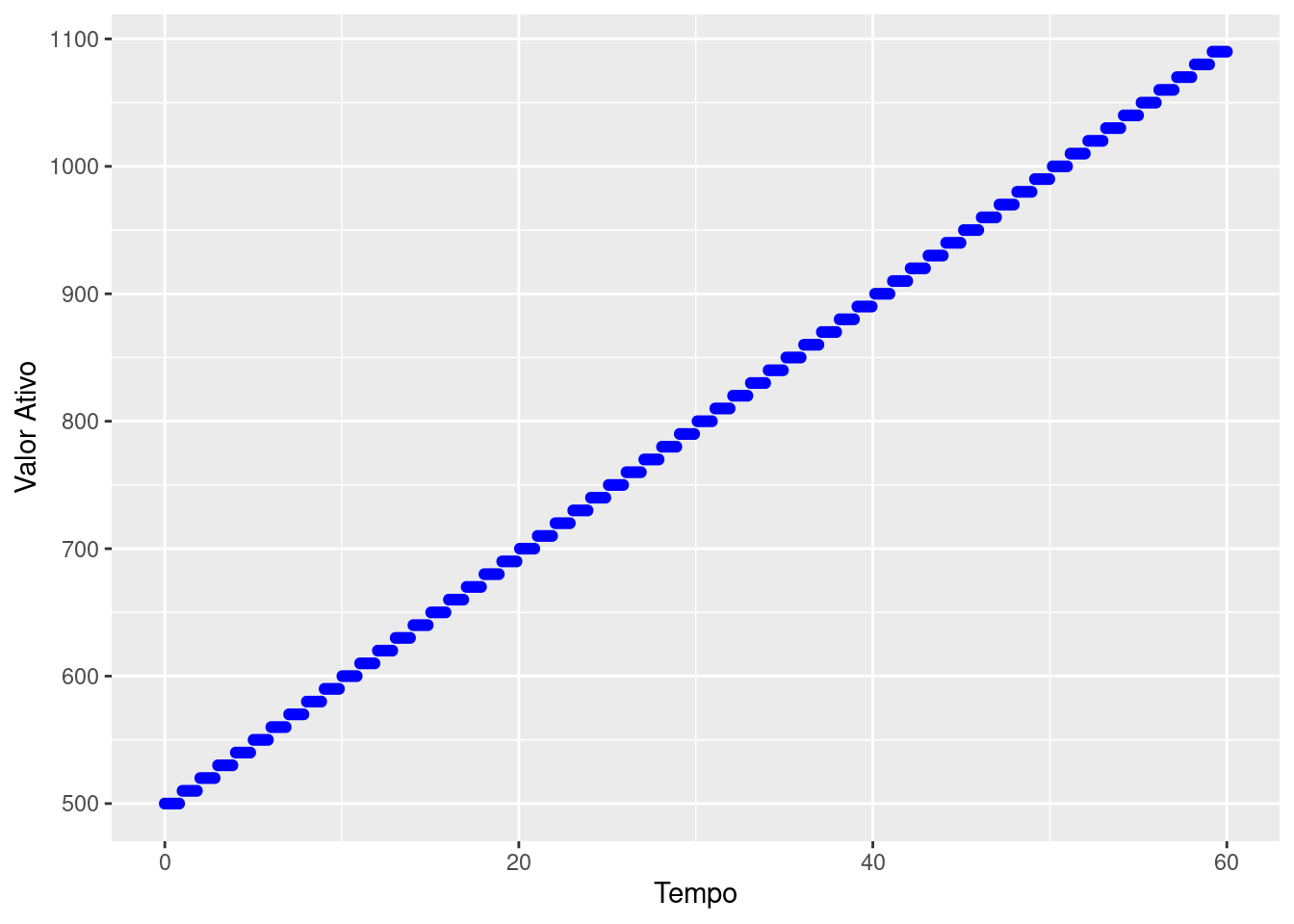
Assim como no caso anterior, o valor do ativo permanece constante até o momento de sua remuneração. No entanto, note que a curva possui agora um comportamento linear e não mais exponencial. A curva do valor do ativo é muito próxima ao gráfico da Figura 1.2 quando o ativo é capitalizado continuamente, mas tendo como referência o valor aplicado inicialmente para sua remuneração.
1.8 Conclusão
Na última seção vimos os regimes quando estes são capitalizados continuamente e discretamente. Em cada um deles abordamos duas situações distintas onde a referência para o valor da remuneração situa-se ou no valor atual ou inicial do ativo. No caso em que a remuneração é proporcional ao investimento inicial temos o que é chamado de regime de juros simples. No outro caso, temos o chamado regime de juros compostos. No que tange o período de capitalização, iremos tratar ao longo do curso apenas do caso discreto. Na próxima seção vamos abordar brevemente o regime de juros simples (caso discreto). Na sequência vamos estudar com mais detalhes o caso que é mais comum no mercado, que é o regime de juros compostos (caso discreto).
1.9 Exercícios
Exercício 1.1 A família Silva é muito próxima da família Matos. Durante um período de crise financeira dos Matos, os Silvas fizeram o primeiro empréstimo aos Matos em janeiro de 2023 no valor de 10.000. Em março a família Matos recorreu novamente a um empréstimo no valor de 30.000, porém dessa vez metade do recurso foi enviado pelos Silvas, enquanto a outra parte foi proveniente do Banco Paiva. Em maio, os Matos realizaram o pagamento da metade do primeiro empréstimo concedido pelos Silvas. No mês de julho os ventos mudaram e a família Matos saiu da crise. No mesmo mês os Matos pagaram a segunda metade do primeiro empréstimo e adiantaram o pagamento do restante da dívida com os Silvas. No entanto, a dívida com o Banco Paiva não quitada. No mês de agosto a crise chega para os Silvas, além de problemas financeiros a ala da família chamada de Silva Corrêa se dividiu do restante da família chamada de Silva Braga. Em outubro, os Silva Corrêa fazem pedidos de empréstimos para o Banco Paiva no valor de 20.000, para a família Matos no valor de 28.000,00 e para os Silva Braga no valor de 350,00. No mês de novembro a família Matos liquida sua dívida com o Banco Paiva. No final do ano, os Silva Corrêa ganham um processo contra os Silva Braga no total de 40.000,00. No entanto, apenas 25% do valor do processo será pago em 2023.
Diante dessa história construa os seguintes diagramas de fluxo de caixa no ano de 2023 para os seguintes agentes:
Família Matos
Família Silva
Banco Paiva
Família Silva Corrêa
Família Silva Braga
Deixe claro qual o padrão adotado na construção do diagrama. O mesmo padrão deve ser usado em todos os itens.
Em breve
Dexter e Didi querem investir R$500,00 para poder comprar um Drone no mês de julho. Dexter opta por investir em ações enquanto Didi em renda fixa. O valor da ação durante o período foi de R$50,00 no mês março, R$45,00 no mês abril, R$55,00 no mês maio e R$53,00 no mês junho. O título de renda fixa que possui a função \(\psi(t,v_{0})=V_{0}e^{0.02t}\) em que \(t\) representa o mês. Mostre qual dos dois teve a melhor rentabilidade.
Dexter: \(500\cdot\left(1+\frac{53-50}{50}\right)=530\)
Didi: \(500\cdot e^{0.02\cdot3}=530.92\)
Exercício 1.2 Suponha que Zé Colméia possua uma função utilidade para seu consumo de potes de mel dada por \[ u(x,t) = \alpha x-\beta t, \] onde \(\alpha,\beta>0\), \(t\) e \(x\) são os números meses e potes de mel respectivamente. Sabemos que quando Zé Colméia consome 2 potes de mel ele tem uma utilidade de 40 e consumir um pote amanha é de 19. A partir dessas informações, qual deveria ser a taxa de juros ao mês para que Zé Colméia abra mão de um pote de mel?
A taxa de juros deve ser o valor no qual Zé Colméia fique indiferente entre consumir um pote de Mel agora ou consumir posteriormente.
\[ \begin{align} u(x+a,t+1) & = u(x,t). \end{align} \]
Logo,
\[ \begin{align} \alpha(x+a)-\beta(t+1) & = \alpha x - \beta t\\ \alpha x+\alpha a-\beta t-\beta & = \alpha x - \beta t\\ \alpha a & = \beta\\ \Rightarrow a & = \frac{\beta}{\alpha}.\\ \end{align} \] Sabemos que \(u(2,0)=40\), então
\[ \alpha\cdot 2 - \beta\cdot 0 = 40 \Rightarrow \alpha = 20. \]
Sabemos também que \(u(1,1)=19\), então
\[ \begin{align} \alpha\cdot 1-\beta\cdot 1 & = 19\\ \beta & = \alpha - 19\\ \Rightarrow \beta & = 1 \,\,\,\ \text{ pois }\alpha=20. \end{align} \]
Supondo que o pote de mel custe \(p_{M}\), então podemos interpretar o conceito de juros, à luz do exemplo, como o valor em que deve ser adicionado a um pote (\(x=1\)) para cada pote que foi deixado de ser consumido no instante zero.
\[ \begin{align} i & = \frac{\overbrace{p_{M}\cdot(x+a)}^{\text{valor prox. mês}}}{\underbrace{p_{M}\cdot x}_{\text{valor agora}}}-1=\frac{(x+a)}{ x}-1\\ i & =\frac{(1+a)}{ 1}-1 \,\,\,\text{em que } x=1\\ \Rightarrow i & = a = \frac{\beta}{\alpha} = \frac{1}{20} \end{align} \] Como \(a=\beta/\alpha=0,05\) então a taxa de juros minimamente necessária para Zé Colméia deixar de consumir um pote de mel agora é 5% ao mês. Note também que esse valor é independente do preço do pote de mel.
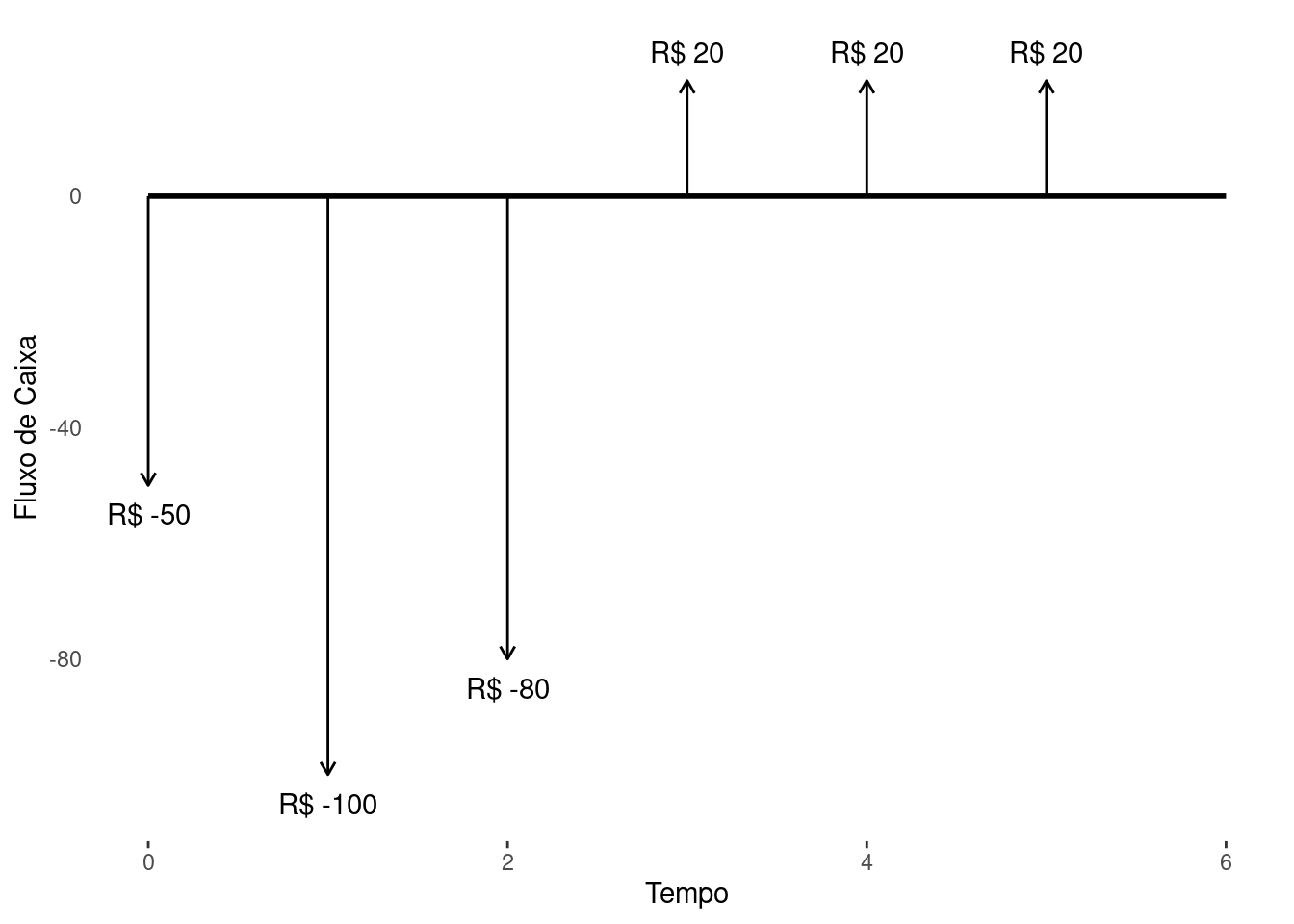
Exercício 1.3 Uma empresa tem um projeto de investir na compra de uma máquina de produzir camisas. O valor da máquina somado aos gastos de instalação é de R$ 250 mil. Ela pode ser adquirida com uma entrada de R$ 50 mil e o restante em 2x de R$ 100 mil. Após sua compra é possível entrar em operação para começar as vendas das camisas em 1 mês.
Sabe-se que a máquina gera um fluxo de caixa positivo de R$ 20 mil por mês referente a sua produção. Com base nestas informações monte o diagrama de fluxo de caixa para este projeto de investimento.
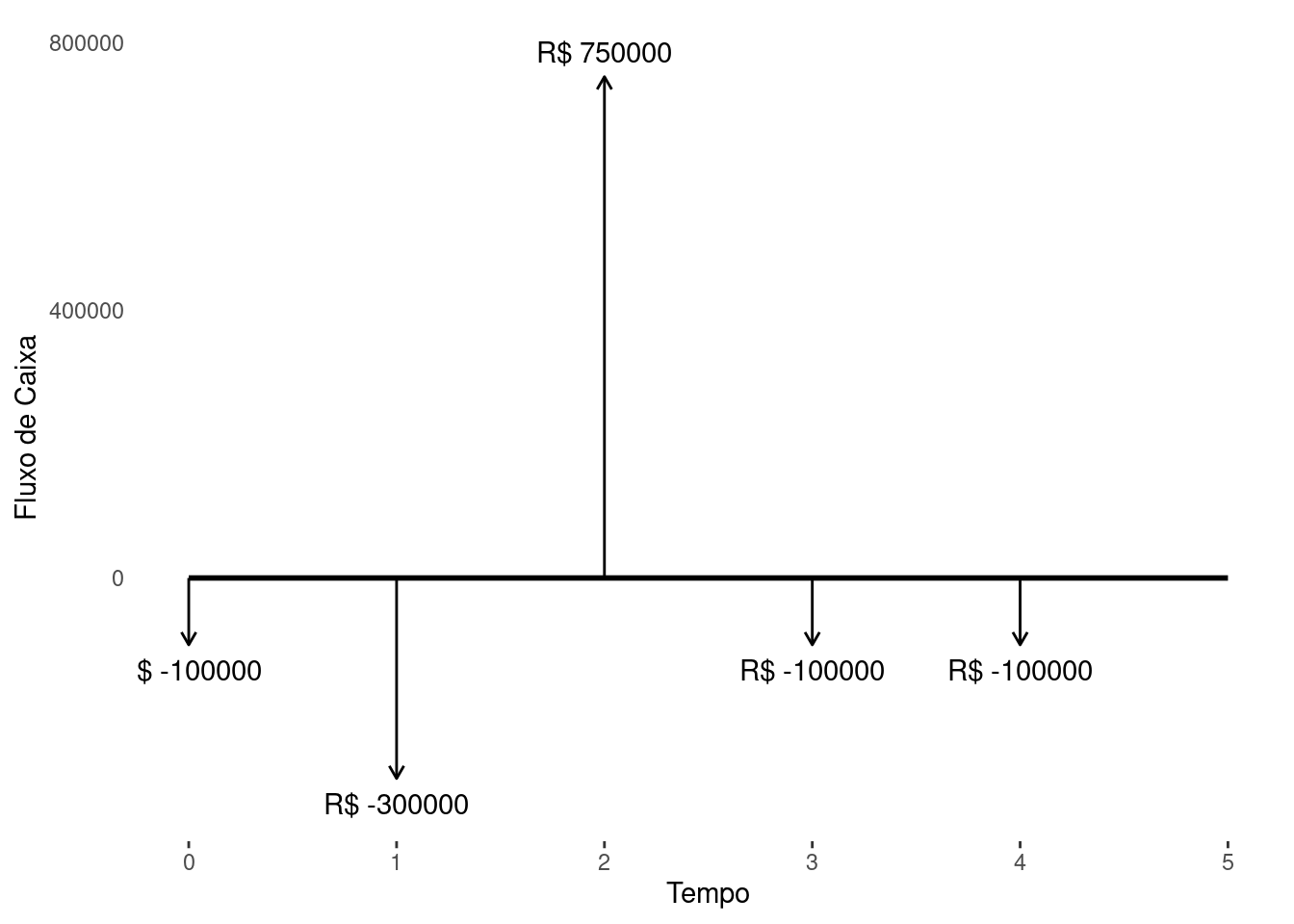
Exercício 1.4 O setor financeiro de uma empresa de evento analisa a viabilidade de um determinado show. Neste evento a empresa responsável pela montagem dos equipamentos e contratação de pessoal cobra 5x de 100 mil reais sendo a 1ª parcela dois mês antes do evento. A equipe dos artistas recebem 50% com 1 mês antecedência e o restante no dia do evento, totalizando 400 mil reais.
Os ingressos são vendidos à vista no valor de 350 reais e tem início 1 mês antes do evento. O local pretendido para o evento tem capacidade máxima de 3000 pessoas. A expectativa é de casa lotada para o evento.
A partir das informações monte o diagrama de fluxo de caixa desse projeto.
Determine qual demanda por ingresso será possível afirmar que o projeto não é interessante do ponto de vista financeiro.
Se a capacidade máxima do local for reduzida para 2500. A resposta do item anterior permanece a mesma?
Uma condição necessária porém não suficiente para que um projeto seja viável é que a quantidade de entrada de recurso supere a quantidade de saída. Quando há mais entrada do que saída temos \(VPL>0\) e quando temos mais saídas do que entrada \(VPL<0\). Para verificarmos se o projeto é viável precisamos somar as entradas e subtrair as saídas. No entanto, como vimos anteriormente, só podemos somar valores quando a data de referência é a mesma. Vimos também que o valor de um ativo em uma data futura deve ter seu valor maior no futuro do que na data presente. Deste modo, o valor atual equivalente a \(300.000\) no próximo mês deve ser um valor ligeiramente menor digamos \(300.000-h_1\), onde \(h_1\) é a diferença entre ter esse valor agora ou esperar um mês. Seguindo esse mesmo raciocínio, vamos aplicar para todos os meses a frente de maneira a busca seu valor equivalente para o momento atual, \(t_{0}\). Com isso estamos aptos a somar e subtrair valores de forma a computar o saldo final.
\[ \begin{align} VPL = &\underbrace{-100.000}_{t_0} +\underbrace{(-300.000 - h_1)}_{t_1} +\underbrace{(750.000 - h_2)}_{t_2} \\ & + \underbrace{(-100.000 - h_3)}_{t_3} + \underbrace{(-100.000 - h_4)}_{t_4} ,\,\,\ h_j \geq 0\\ = & -100.000 -300.000 - h_1 +750.000- h_2 \\ &-100.000 - h_3 -100.000 - h_4 \\ = & 150.000 - (h_1 + h_2 + h_3 + h_4) \\ \end{align} \]
Mesmo sem saber os valores de \(h_1\), \(h_2\), \(h_3\) e \(h_4\) sabemos que a soma de entradas e saídas são \(150.000\) menos os descontos em razão de trazer todos os valores para a data presente. Para que o projeto seja viável a soma \(h_{T}=h_1+h_2+h_3+h_4\) não pode ser maior que \(150.000\), caso contrário, o saldo final será negativo.
\[
\begin{align}
0 \leq VPL \Longleftrightarrow 0 & \leq 150.000 - h_T ,\,\,\ \text{onde } (h_{T} = h_1 + h_2 + h_3 + h_4)\\
\Rightarrow h_T & \leq 150.000 \\
\end{align}
\] Suponha que a demanda seja reduzida para \(2571\) pagantes. Então o saldo no dia evento será \(599.850 = 2571\cdot350-300.000\). Para trazer a valor presente teremos que reduzir seu valor pela quantidade \(h_2\), isto é, \(599.850-h_2\). Considerando todos os meses temos
\[
\begin{align}
VPL = & -100.000 -300.000 - h_1 +599.850- h_2 \\
&-100.000 - h_3 -100.000 - h_4 \\
= & -150 - (h_1 + h_2 + h_3 + h_4). \\
\end{align}
\] Neste caso, por menor que seja os valores de \(h_1\), \(h_2\), \(h_3\) e \(h_4\) ainda assim teremos \(VPL<0\). Porém, caso a demanda seja de apenas uma pessoa a mais, isto é, \(2572\) pagantes. Então o saldo no dia evento será \(600200=2572\cdot350-300.000\). Refazendo os mesmos cálculos \[
\begin{align}
VPL = & -100.000 -300.000 - h_1 +600.200- h_2 \\
&-100.000 - h_3 -100.000 - h_4 \\
= & 200 - (h_1 + h_2 + h_3 + h_4). \\
\end{align}
\] Diferente do caso anterior, caso a soma \(h_{T}=h_1+h_2+h_3+h_4\) seja menor de \(200\) então o projeto será viável. Ainda que não saibamos o valor de \(h_T\), sabemos que ainda há uma possibilidade do \(VPL\) ser positivo e podemos ficar em dúvida. No entanto, isto não ocorre no caso anterior, onde temos certeza que o projeto é inviável.
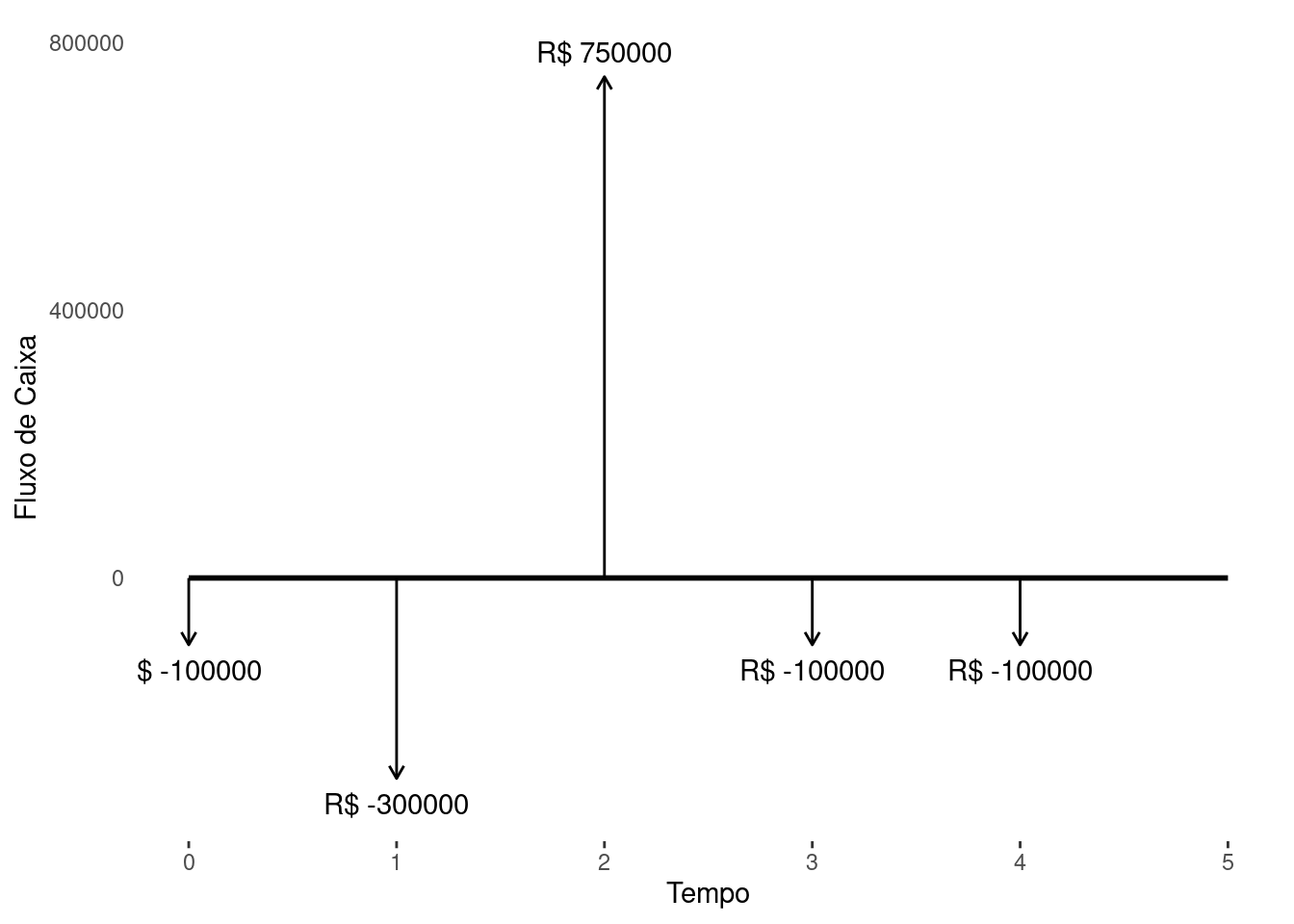
Pelo item anterior vimos que com 2571 pagantes o projeto certamente é inviável. Novamente, note que mesmo sem saber os valores de \(h_{T}\) sabemos que o projeto com menos de 2571 é inviável.
