5 Revisão Matemática Básica

Os objetivos deste capítulo consistem em revisar brevemente os conceitos e métodos matemáticos elementares que serão utilizado como ferramental chave para abordar os problemas no âmbito da matemática financeira. Apesar de instrumentos como planilhas eletrônicas e calculadoras financeira, como a Hp12c, serem amplamente difundidos, sua disponibilidade de nenhuma maneira substitui a necessidade do conhecimento dos métodos matemáticos. A principal razão para isso se funda no próprio objeto de estudo da disciplina, que é a área de finanças, no qual são descritos e modelados seus problemas juntamente com suas definições e conceitos atraveś da própria linguagem matemática. Ademais, esses instrumentos cumprem apenas o papel de execução de rotinas e operações numéricas que só encontram sentido após a definição e expressão de um problema bem definido. Portanto, a compreensão dos elementos básicos de matemática cumprem um papel indispensável para adentrarmos no campo da matemática financeira e aproveitar tudo o que ela tem a nos oferecer.

5.1 Funções

No âmbito da matemática, uma função, que aqui denominaremos pela letra $f$, é um objeto que descreve uma relação entre dois conjuntos, dado por uma relação de correspondência entre os elementos de um conjunto $A$ com os elementos de um conjunto $B$. Para que uma relação entre o conjunto $A$ e $B$ seja dita uma função, cada elemento do conjunto $A$ que for relacionado deve ter um ÚNICO correspondente no conjunto $B$. Importante, repare que nada foi dito sobre um elemento de $B$ possuir mais de um correspondente em $A$. O conjunto $A$ é chamado de domínio e o conjunto $B$ de contradomínio.

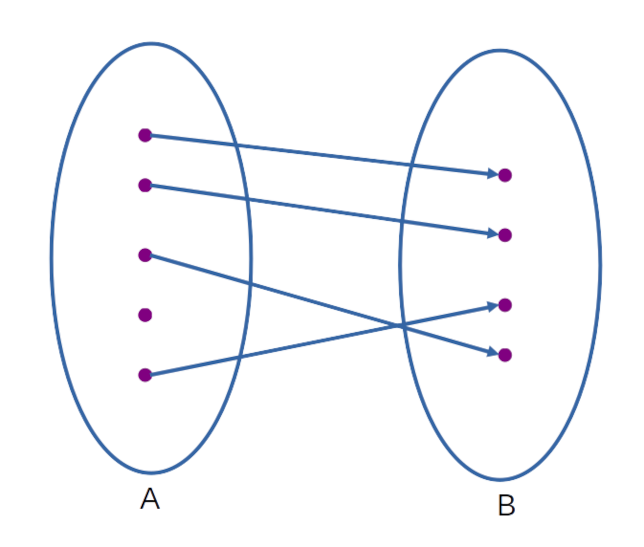
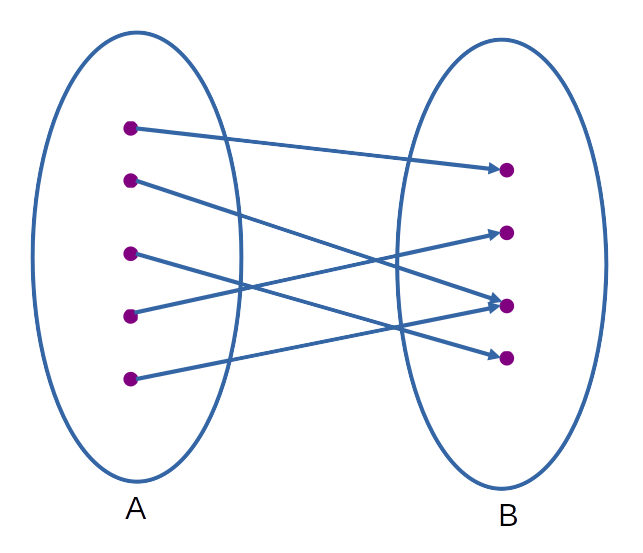
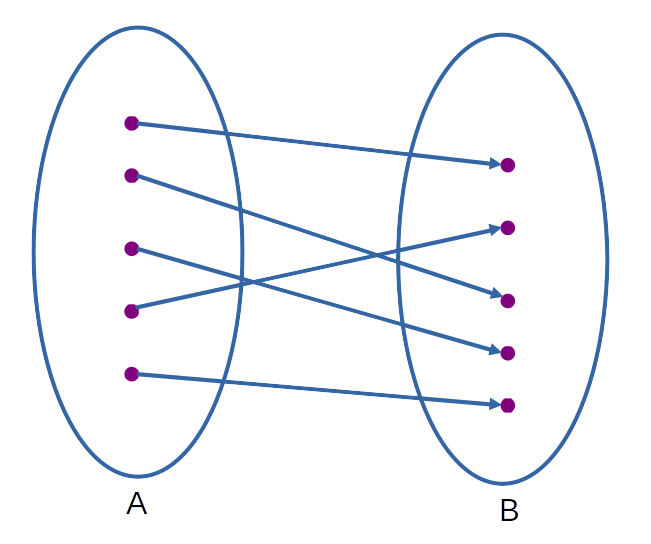
Função $f$, domínio $A$ e contradomínio $B$: $f: A \rightarrow B$.

linx = transpose(lindbx)
liny = linx.map((t) => {
        t.y = la*t.x+lb
        return (t)
})
viewof la = Inputs.range([-5, 5], {label: "Coeficiente a", value: 2, step: 0.25, placeholder: "-5 5"})
viewof lb = Inputs.range([-5, 5], {label: "Coeficiente b", value: 1, step: 0.25, placeholder: "-5 5"})
Plot.plot({
y: {
    color: {legend: true},
    grid: true,
    domain: [-15, 15],
  },
x: {domain: [-8, 8]},
  marks: [
    Plot.ruleY([0]),
    Plot.ruleX([0]),
    Plot.lineY(liny, {x: "x", y: "y", stroke: "#4CF30C", strokeWidth: 3, curve: "catmull-rom"})
  ]
})

Exemplo: função linear (1º grau, afim) $f: \mathbb{R} \rightarrow \mathbb{R}$

Uma função linear é uma função na qual seu gráfico é representado por uma linha reta. Ela também pode ser vista como uma função polinomial de grau um ou zero. O polinômio de grau 2 será abordado na sequência. Tanto domínio quanto o contradomínio de uma função linear são os conjunto dos números reais $\mathbb{R}$ e denotamos por $f: \mathbb{R} \rightarrow \mathbb{R}$. Sua forma funcional é dada por

\[ f(x)=ax+b, \]

onde $a,b\in\mathbb{R}$. O termo $a$ que multiplica a variável $x$ é chamado de coeficiente angular e a constante $b$ é conhecida como coeficiente linear. O coeficiente $a$ é assim chamado porque ao mudar seu valor, ele provoca um mudança na inclinação da reta. Já o coeficiente linear, quando alterado, causa um deslocamento no sentido vertical sobre a reta. Para visualizar esses efeitos sobre a reta, manipule os valores dos coeficientes $a$ e $b$ no painel abaixo e verifique os efeitos causados no gráfico.

Uma variável $y$ descrita em termos de uma função linear $y=f(x)$ tem a propriedade de sempre responder proporcionalmente a mudança no valor de $x$. Esse comportamento é facilmente percebido ao observar o comportamento do seu gráfico. Sendo um pouco mais preciso, se a variável originalmente em um certo patamar $x_{1}$ for descolada para um outro $x_{2}=x_{1}+h$, em uma distância $h$, irá provocar

\[ \begin{align} y_{2}&=ax_{2} + b=a(x_{1}+h) + b \,\,\,\, \text{(Subst } x_{2}= x_{1}+h\text{)}\\ &=ax_{1}+b+hb=y_{1}+ah \end{align} \]

Repare que ao ser acrescido $h$ na variável $x_1$ houve um crescimento em $y$ proporcional a $h$ ($y_{1}\mapsto y_{1} +a h$). Em síntese, um acréscimo de $h$ em $x$ provocará um acréscimo de $ah$ em $y$. Um ponto interessante é que essa relação se mantém independente do ponto avaliado em $x$. Logo se partir do ponto $x_{1}=10$ para o ponto $x_{2}=10+h$ ($x_{2}-x_{1}=h$) teremos $y_{2}=a\cdot(10+h)+b=y_1+ah$ ou mesmo do ponto $x_{1}=300$ para o ponto $x_{2}=300+h$ $y_{2}=a\cdot(3000+h)+b=y_1+ah$ resultará no mesmo.

Apesar de simples, as funções lineares mostram o quão poderosas podem ser ao permitir tratar diversos problemas diretamente ligados a gestão corporativa, indo desde logística até a parte financeira. Para demonstrarmos isso, considere o exemplo a seguir sobre estrutura de custo e alavancagem operacional de uma fábrica. Neste exemplo, os conceitos e ferramentas de funções lineares serão imprescindíveis.

Exemplo 5.1 A direção de uma fábrica de médio porte de manequins contrata um consultor para ajuda-la no estudo de viabilidade de transição da tecnologia empregada no maquinário da fábrica. Ao analisar a estrutura de produção da fábrica, o consultor obtém as seguintes informações

A maioria dos maquinários não desliga salvo para manutenção. Quando não estão em produção, eles ficam em standby.
Há sempre pelo menos uma equipe nas dependências da fábrica e o que inclui todos os turnos.
O histórico recente mostra que no primeiro trimestre do ano houve um bom volume de vendas da ordem de 480 mil totalizando 1200 peças vendidas. O mesmo não se verificou para o trimestre seguinte. A Tabela 5.1 exibe um resumo destes dados.

Tabela 5.1: Indicadores Contábeis.

1.Trimestre 2.Trimestre

Receita 480,000.00 -18%

Lucro Bruto 168.75 114750

Produção 1,200.00 984

Preco Unid 480.00 400

Indicadores.
A empresa está muito inclinada a fazer uma grande aquisição de novos maquinários com tecnologia chinesa. Parte dessa motivação nasce da preocupação com movimentos de empresas concorrentes do setor que estão aderindo a esses novos aparelhos. Aparentemente, esses concorrentes estão conseguindo ampliar seus marketing share, em razão do aumento de suas margens de lucro bruto.
Um levantamento mais cuidadoso do consultor apontou para uma elevação dos gastos de manutenção, contratação de pessoal especializado, e equipe de suporte e seguro proteção na hipótese de aquisição dos novos equipamentos. Outro fator é o maior consumo de energia em virtude dos novos aparelhos demandarem maior consumo do que o atual sistema. A estimativa de aumento das despesas fixas mensais é de 25 mil reais.
A tecnologia desses novos aparelhos oferecem um ganho de desempenho em função do aumento de velocidade de giro de processos e eliminação de alguns processos. Outro fator atraente dos novos aparelhos é a redução considerável de desperdício. Diante disso, os engenheiros estimam uma melhoria da produtividade de 20% quando comparada ao maquinário instalado de tecnologia norte americana.

	1.Trimestre	2.Trimestre
Receita	480,000.00	-18%
Lucro Bruto	168.75	114750
Produção	1,200.00	984
Preco Unid	480.00	400

Para demonstrar a construção da função lucro e os conceitos atrelados, vamos tomar como ponto de partida o exemplo da fábrica. Deste modo, podemos descrever o comportamento de ganhos da fábrica através de duas funções: a função receita e a função custo. A receita deve ser expressa por uma função linear $s_{p}$ mantido a os preços fixos. Quando dobramos as unidades vendidas o mesmo deve acontecer com a receita, $s_{p}(2\cdot x)=2s_{p}(x)$. Adicionalmente a função deve possuir o comportamento de ser zero quando a quantidade vendida $x$ também é zero, isto é, $s_{p}(0)=0$ Uma função que atende aos requisitos é

\[ s_{p}(x)=px. \tag{5.1}\]

O coeficiente angular $p$ da função linear $g$ representa o preço unitário. Na ilustração da fábrica vamos assumir o preço de venda unitário constante e independente da quantidade vendida. Como vimos anterior e sendo tanto quanto intuitivo, este coeficiente reflete o grau de inclinação da reta da receita. A segunda função deve descrever o comportamento dos custos em função da quantidade produzida. Há basicamente dois tipos de custos ligado a produção, os custos variados e os custos fixos. Os variados são os custos intrinsecamente ligado a fabricação ou aquisição do produto. Deste modo, não existindo venda ou produção, não há a sua ocorrência. Já os custos fixos são aqueles que são invariáveis pela quantia produzida. Ela é também mantida constante dentro de um certo intervalo de produção ou venda. Nesta perspectiva, a curva de custo é composta por ambos os tipos. No caso da fábrica de manequim vamos considerar o custo unitário de produção constante igual a $cv$.

\[ \begin{align} c(x)&=cv\cdot x+cf. \end{align} \tag{5.2}\]

De posse das funções 5.1 e 5.2 podemos caracterizar a função lucro a partir da diferença entre as duas.

\[ \begin{align} l(x)&=s_{p}(x)-c(x)\\ &=p\cdot x -cv\cdot x - cf\\ &=(p-cv)x-cf\\ &=m\cdot x-cf. \end{align} \tag{5.3}\]

O coeficiente $m=p-cv$ é denominado margem de contribuição. Seu valor refere-se a porção do preço unitário destinada para contribuir ou financiar os custos fixos. A porção restante é utilizada para bancar o custo direto, isso é, o custo variável. A quantidade vendida que acarreta lucro zero é computada igualando $l(x)$ a zero

\[ \begin{align} l(x)=0 &\Leftrightarrow m \cdot x - cf=0\\ & \Rightarrow x=\frac{cf}{m}=br.\\ \end{align} \tag{5.4}\]

A quantia encontrada na equação acima denominada ponto de equilíbrio ou breakeven e possui uma interpretação econômica interessante. Ela indica o volume de vendas a partir do qual a empresa passa a ter lucro bruto. Na ponta contrária, a quantidade de vendas abaixo do breakeven representará prejuízo a empresa.

Pelos dados da Tabela 5.1 levantado pelo consultor encontramos a quantia total produzida no 2 trimestre $0.82\cdot 1200 = 984$ e a sua receita dada por $0.82\cdot 480000 = 393600$. Os valores das margens de contribuição $m$ e dos custos fixos $cf$ são estimados através do sistema de equações lineares 5.5 obtido pela Função 5.3 aplicada a cada trimestre com as informações da Tabela 5.1. Uma breve explanação da construção da função lucro é encontrada clicando no botão acima.

\[ \begin{align} 168750 &= m\cdot 1200-cf\\ 114750&=m\cdot984-cf. \end{align} \tag{5.5}\]

O sistema é resolvido realizando a subtração da 1ª equação pela 2ª obtém-se a margem de contribuição com valor $m=250$. Substituindo $m$ por qualquer das equações, encontra-se o custo fixo de $cf=131250$. Logo, a fábrica tem breakeven no valor de $br=525$ com sisteestes é de . Seu valor indica quantidade necessária para ser vendida para custear o custo fixo integralmente. As quantias acima deste ponto passam a remunerar os acionistas ou outras atividades da empresa que não passem direto para o resultado. Seu cálculo é feito dividindo o total de custos fixos pela margem de contribuição do produto. No caso da fábrica $be = \frac{cf}{m}$ resulta em 525, ou seja, a fábrica necessita vender ao menos esta quantia para não ter prejuízo.

Com todos os valores destes parâmetros podemos enxergar os ganhos de produção da fábrica

Por questões didáticas a construção do exemplo conta uma uma simplificação diante de uma realidade complexa que é uma industria. No entanto, os princípios dos desafios de uma fábrica ou mesmo comercial estão presente no exemplo.

se para todo $x$ for acrescido uma constante $k$, a variável $y$ continua sendo uma função linear de $x$. adicionarmos o valor de $k$ a variável $x$, ao valor possui as seguintes propriedades:

Seja $d\neq 0$ uma constante $f(d\cdot x) = d$ tem a propriedade de sempre responder de forma proporcional.

seriex = transpose(dbx)
seriey = seriex.map((t) => {
        t.y = a*Math.pow(t.x,2)+b*t.x+c
        return (t)
})
viewof a = Inputs.range([-5, 8], {label: "Coeficiente a", value: 2, step: 0.25, placeholder: "-5 5"})
viewof b = Inputs.range([-5, 8], {label: "Coeficiente b", value: -1, step: 0.25, placeholder: "-5 5"})
viewof c = Inputs.range([-5, 8], {label: "Coeficiente c", value: -2, step: 0.25, placeholder: "-5 5"})
Plot.plot({
y: {
    color: {legend: true},
    grid: true,
    domain: [-25, 25]
  },
x: {domain: [-10, 10]},
  marks: [
    Plot.ruleY([0]),
    Plot.ruleX([0]),
    Plot.lineY(seriey, {x: "x", y: "y", stroke: "#544FC5", strokeWidth: 3, curve: "catmull-rom"})
  ]
})

Exemplo: função quadrática (2º grau) $f: \mathbb{R} \rightarrow \mathbb{R}$
\[ f(x)=ax^2+bx+c. \]

serieex = transpose(dbex)
serieey = serieex.map((t) => {
        t.y = be*Math.exp(ae*t.x)
        return (t)
})
viewof ae = Inputs.range([-5, 5], {label: "Coeficiente a", value: 2, step: 0.25, placeholder: "-5 5"})
viewof be = Inputs.range([-5, 5], {label: "Coeficiente b", value: 2, step: 0.25, placeholder: "-5 5"})
Plot.plot({
y: {
    color: {legend: true},
    grid: true,
    domain: [-10, 20]
  },
x: {domain: [-1, 3]},
  marks: [
    Plot.ruleY([0]),
    Plot.ruleX([0]),
    Plot.lineY(serieey, {x: "x", y: "y", stroke: "#EF6606", strokeWidth: 3,curve: "catmull-rom"})
  ]
})

Exemplo: função exponencial $f: \mathbb{R} \rightarrow \mathbb{R}$
\[ f(x)=b e^{ax}. \]

serielgx = transpose(dblgx)
serielgy = serielgx.map((t) => {
        t.y = lga*Math.log(lgb)*Math.log(t.x) 
        return (t)
})
viewof lga = Inputs.range([-5, 5], {label: "Coeficiente a", value: 2, step: 0.25, placeholder: "-5 5"})
//viewof lgb = Inputs.range([1, 10], {label: "Coeficiente b", value: 2.718282, step: 0.25, placeholder: "1 10"})
viewof lgb = Inputs.radio( new Map([ ["2", 2], ["e", 2.718282], ["10", 10]]), {value: 2.718282, label: "Base b"})
Plot.plot({
y: {
    color: {legend: true},
    grid: true,
    domain: [-5, 5]
  },
x: {domain: [-0.5, 10]},
  marks: [
    Plot.ruleY([0]),
    Plot.ruleX([0]),
    Plot.lineY(serielgy, {x: "x", y: "y", stroke: "#ED0BE1", strokeWidth: 3,curve: "catmull-rom"})
  ]
})

Exemplo: função logarítmica $f: \mathbb{R}^{+} \rightarrow \mathbb{R}$
\[ f(x)= a\log_{b} x. \]

5.1.1 Função Linear

Qual dessas funções tem um comportamento linear? Considere $a,b,c>0$

$f(x)=ax^2+bx+c$
$f(x)=\frac{b}{x}+3x$
$f(x)=a+bx$
$f(x)=be^{2x}$
$f(x)=log(be^{2x})$

5.2 Logarítmo

O logaritmo é de extrema importância na área da matemática financeira. Inúmeros são os casos em que nos deparamos com logaritmos. Ele nos auxilia em diversos cálculos, sobretudo quando estamos interessados em saber quanto tempo uma determinada aplicação precisa para que alcance um certo montante de dinheiro sendo que a variável de interesse está no expoente de uma outra variável. Para manipular casos assim, precisamos entender ou relembrar o que esse logaritmo, tão poderoso, significa.

Na área da matemática, o logaritmo de um número é o expoente no qual outro número fixo, denominado base, tem que ser elevado para computar este número. Em outras palavras, para quaisquer dois números reais $b$ e $c$, onde $b>0$ e $b\neq 1$, o logaritmo de $a$ na base $b$ estabelece

\[ \log_{b}(a)=c \Leftrightarrow a = b^c. \] Para nossos propósitos a função $\log$ está definida apenas para $a>0$. O logaritmo na base 10 $(b = 10)$ é chamado de logaritmo comum. Já o logaritmo na base $e$ ($e\approx 2.718$ constante irracional) é chamado de logaritmo natural. Ele é tão empregado que utilizamos a notação $\ln(x)=\log_{e}(x)$. Quando o valor da base está bem clara então em geral ela é suprimida $\log x=\log_{10}x$. Na área de T.I. e em telecomunicação $\log x=\log_{2}x$.

5.2.1 Propriedades Logarítmo

a. Produto (IMPORTANTE!): Sejam os seguintes logaritmos

\[ \begin{align} \log_{b}x=w' &\Leftrightarrow x = b^{w'}\\ \log_{b}y=w'' &\Leftrightarrow y = b^{w''} \end{align} \]

então,

\[ \begin{align} xy=b^{w'}\cdot b^{w''} = b^{w'+w''} & \Leftrightarrow \log_{b}xy=w' + w''. \end{align} \]

Portanto, $\log_{b}(\boldsymbol{\color{bid}{x}}\cdot\boldsymbol{\color{loan}{y}})=\log_{b}\boldsymbol{\color{bid}{x}} + \log_{b}\boldsymbol{\color{loan}{y}}$.

b. Potência: A $p$-ésima potência de $x$ é escrita como $x^{p}=x \cdot x \cdots=\prod_{i=1}^{p}x$

\[ \begin{align} \log_{b} x^{p}& =\log_{b}\left(x \cdot x \cdots x\right)=\log_{b}\prod_{i=1}^{p}x\\ &= \log_{b}x+\cdots+\log_{b}x = \sum_{i=1}^{p} \log_{b}x \,\,\,\ \text{(Propriedade a.)}.\\ \end{align} \]

Em síntese, temos $\log_{b}x^{\boldsymbol{\color{bid}{p}}}=\boldsymbol{\color{bid}{p}}\cdot\log_{b}x$.

c. Mudança de Base: Suponha $\log_{c} x=z$, para mudar de base $\boldsymbol{\color{bid}{c}} \rightarrow \boldsymbol{\color{loan}{b}}$ partimos da definição

\[ \begin{align} \log_{c} x=z &\Leftrightarrow x = c^{z}\\ \log_{b}x &=\log_{b}c^{z}\\ &=z\cdot\log_{b}c \,\,\, \text{(Propriedade b.)}\\ &=\log_{b}c\cdot\log_{c}x \,\,\,\text{(Substituindo $z$)}. \end{align} \]

Em síntese, $\log_{\boldsymbol{\color{bid}{c}}}x=\log_{\boldsymbol{\color{loan}{b}}}\boldsymbol{\color{bid}{c}}\cdot \log_{\boldsymbol{\color{loan}{b}}}x$.

d. Quociente: Seja a razão $x/y>0$ onde $y\neq 0$.

\[ \begin{align} \log_{b}\left(\frac{x}{y}\right)& =\log_{b}\left(x\cdot y^{-1}\right)\\ &=\log_{b} x +\log_{b} y^{-1} \,\,\, \text{(Propriedade a.)}\\ &=\log_{b} x - \log_{b} y \,\,\, \text{(Propriedade b.)}. \end{align} \]

Em síntese, $\log_{b}\left(\boldsymbol{\color{loan}{x}}/\boldsymbol{\color{bid}{y}}\right)=\log_{b}\boldsymbol{\color{loan}{x}}-\log_{b}\boldsymbol{\color{bid}{y}}$.

5.3 Exercícios

Exercício 5.1 O ativo $P_{t}$ tem seu valor ao longo do tempo descrito de acordo com a equação abaixo. Utilize as propriedades de logaritmo aprendidas no início do capítulo para achar o melhor momento de vender o ativo $P_{t}$, isto é, o momento em que estiver no máximo. A equação do preço deste ativo no tempo $t$ é dado por

\[ P_{t} = b^{t}e^{-at^2+c}. \tag{5.6}\]

Considere o valor de $a=-1.25$, $b=403$ e $c=10$. Uma sugestão é usar os painéis geradores de gráfico disponíveis neste capítulo para auxiliá-lo caso tenha dificuldades.

Utilize as propriedades dos logaritmos apresentadas neste capítulo. Veja se após aplicar as propriedades o valor de $\log(P_{t})$, como função de $t$, se assemelha com algumas das funções apresentadas nos gráficos interativos (linear, quadrática, exponencial, logarítmica).