4 Séries Uniformes
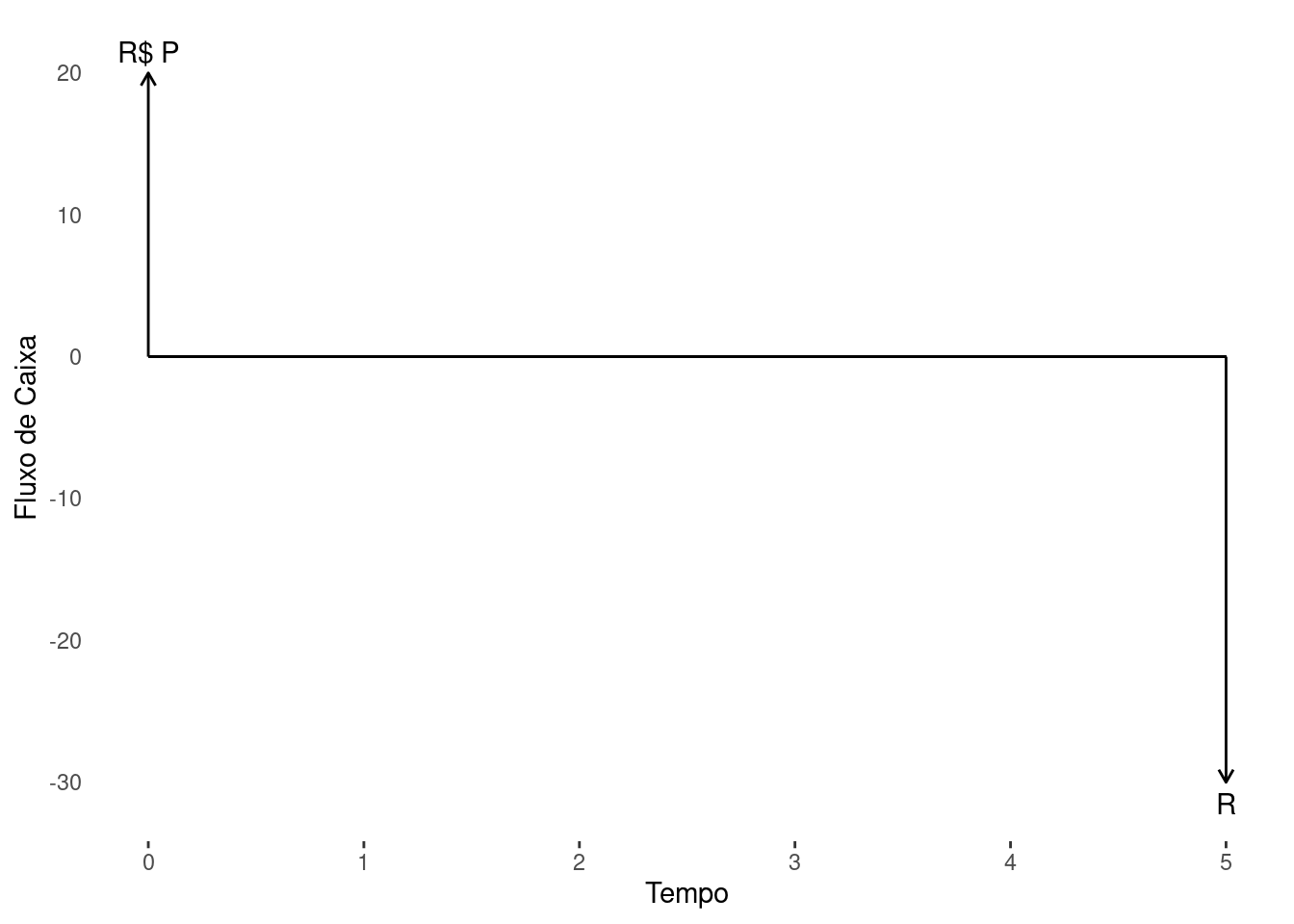
Nos capítulos anteriores, trabalhamos com situações em que o fluxo de caixa é composto por uma entrada e uma saída, sendo elas deslocadas entre si no tempo. Nestas circunstâncias, o valor presente é calculado por meio da fórmula \(PV=FV/(1+i)^n\) e sua operação pode ser ilustrada por meio do diagrama da Figura 4.1 (a). Apesar de simples, esta conformação nos permitiu equacionar diferentes casos. Não obstante, inúmeras outras situações recaem em problemas envolvendo fluxos de caixas com configurações mais diversas, como as dispostas na Figura 4.1. Neste capítulo, vamos abordar o caso em que há pagamentos ou recebimentos sucessivos na avaliação do fluxo de caixa.
Definição 4.1 (Série Uniforme:) Chama-se série uniforme ou anuidade uma sucessão ou sequência de pagamentos (saída de caixa) ou recebimentos (entrada de caixa). As transações ou prestações, representadas por entradas ou saídas de caixa, são denominadas termos de uma série uniforme ou de uma anuidade. Elas são homogêneas e ocorrem em datas preestabelecidas com intervalos regulares de tempo.
O entendimento sobre a mecânica de funcionamento das anuidades adquire especial atenção em virtude de sua ligação com nossa vida cotidiana. As vendas do comércio, por exemplo a prazo, constantemente empregam as séries uniformes como forma de pagamento disponível aos seus clientes. A obra de Paschoarelli (2006) destaca diversos artifícios que são utilizados nas publicidades de comércio e bancos com o intuito de criar ilusões ou distorções na percepção do que efetivamente o consumidor está desembolsando. Vários dos artifícios apontados pelo autor podem ser facilmente evitados com conhecimento sobre anuidades. Iremos trabalhar alguns deles no decorrer do capítulo.
Há modalidades de financiamento habitacional que possui um sistema de amortização da dívida que são série uniforme, como é o caso da conhecida Tabela Price. Mesmo outras modalidades de financiamento como o Sistema de Amortização Constante (Tabela SAC) torna-se mais simples de entender a partir das ideias trabalhadas neste capítulo.
Na primeira seção deste capítulo trataremos das séries finitas. Elas são de suma importância visto que há uma gama de situações envolvendo o meio corporativo, finanças pessoais e também o setor público na qual são aplicáveis. Na segunda seção estenderemos para o caso de séries perpétuas no qual há infinitas transações. As séries uniformes infinitas são empregadas na precificação de ações, mensuração do custo de capital, avaliação de imóveis e dentre outras aplicações. Seguindo a praxe dos demais capítulos, nas resoluções de diversos exemplos e exercícios dispõe de solução numérica por meio da calculadora financeira Hp12-c.
4.1 Séries Uniformes Finitas
Mediante o vencimento da primeira prestação da série uniforme, podemos classificá-la de três formas distintas:
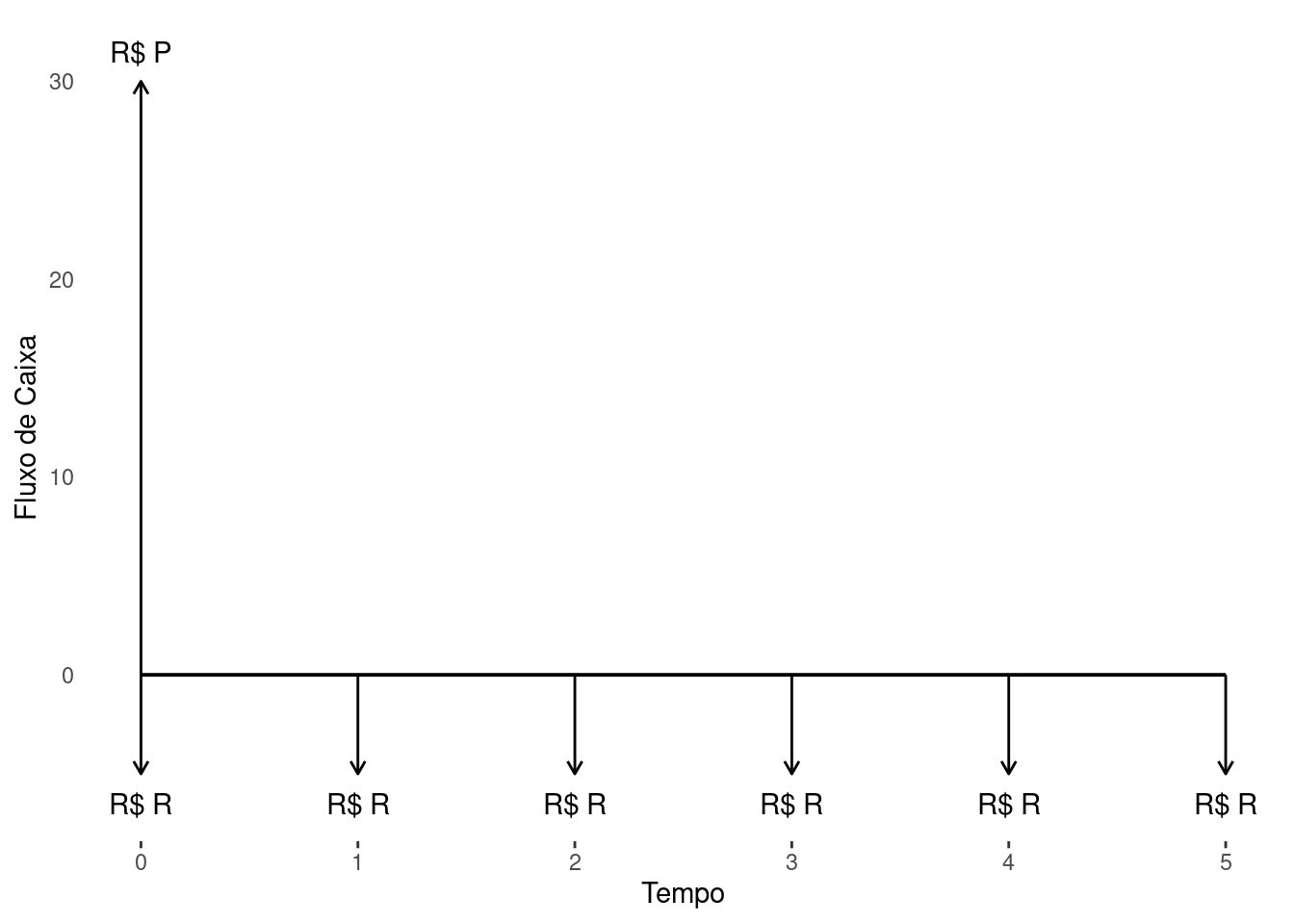
Antecipadas: quando a data da primeira parcela ou prestação ou carnê coincide com a data do empréstimo (com entrada \(R_{0}\)), ou seja, \(R_{0}>0\).
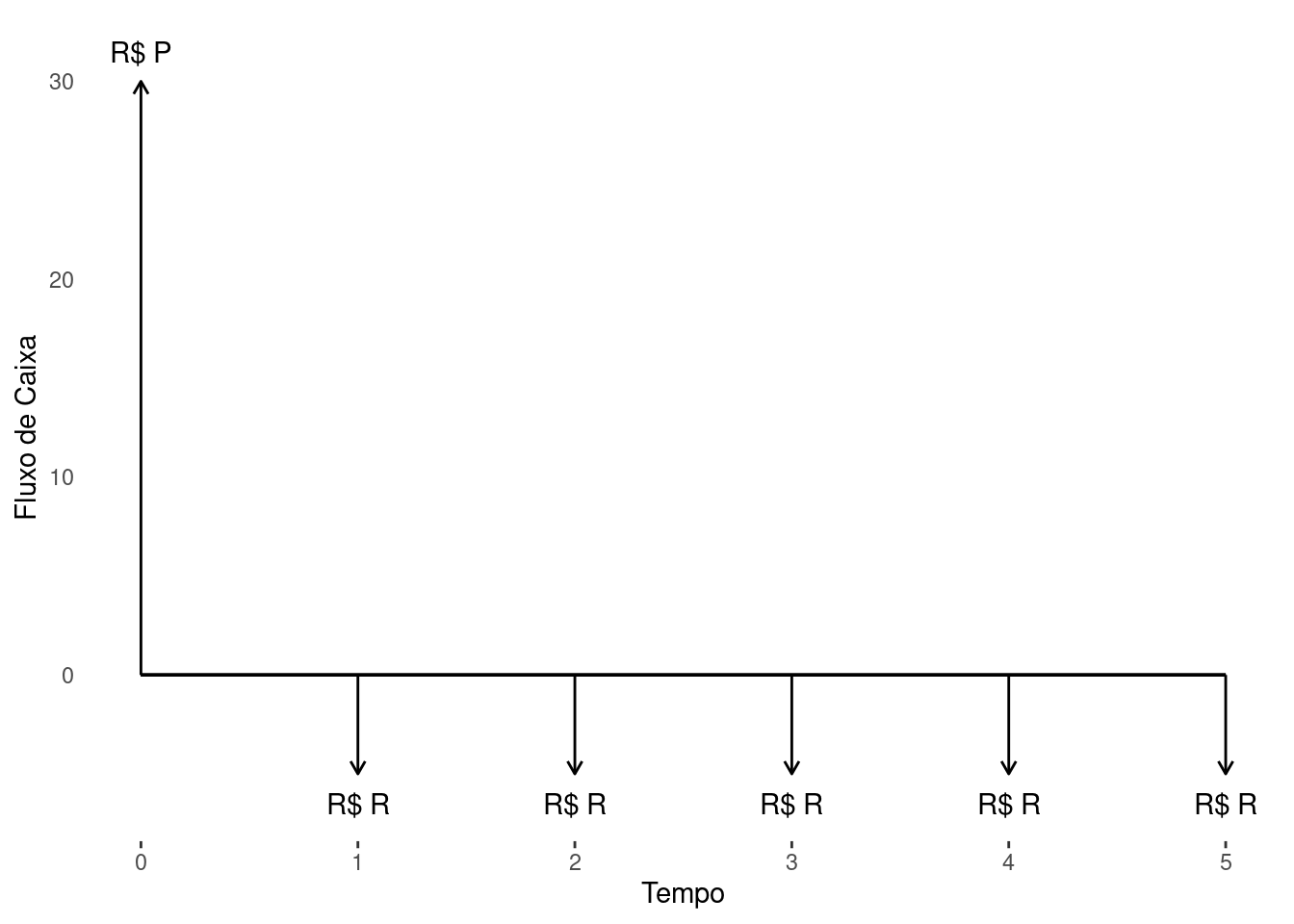
Postecipadas: quando a data de vencimento da primeira parcela ou prestação ou carnê (termo) ocorre 1 período após a data do empréstimo (sem entrada \(R_{0}\)), ou seja, \(R_{0}=0\).
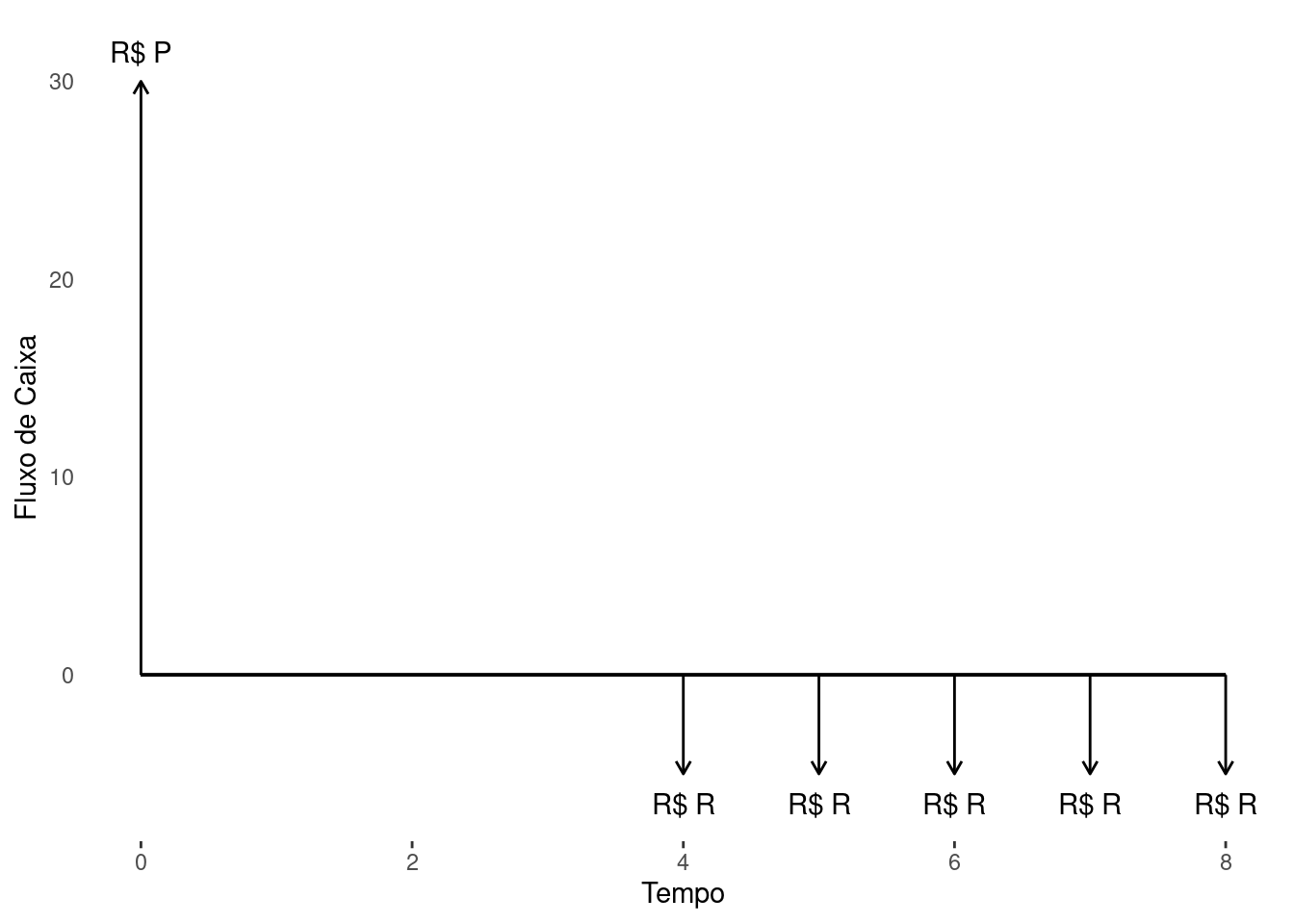
Diferidas: quando a data da primeira parcela ou prestação ou carnê ocorre mais de um período, \(m>1\), após a data do empréstimo (com carência), ou seja, \(R_{0},R_{1},...,R_{m}=0\).
Cada uma dessas formas estão representadas nas Figura 4.1 (b), Figura 4.1 (c), Figura 4.1 (d) respectivamente. Para toda e qualquer série de pagamentos, denomina-se valor presente \(PV\) ou principal \(P\) de um fluxo de caixa a soma dos valores presentes dos seus termos descontados a uma determinada taxa de juros, \(i\), e para um dado ponto focal. Assim sendo, para séries antecipadas temos
\[ \begin{align} P'&= R_{0}+\frac{R_1}{(1+i)}+\frac{R_2}{(1+i)^2}+\cdots+\frac{R_{n-1}}{(1+i)^{n-1}}+\frac{R_n}{(1+i)^{n}}\\ P'-R_{0}&=\sum_{t=1}^{n}\frac{R_{t}}{(1+i)^{t}}. \end{align} \tag{4.1}\]
Sendo \(R_t=R\) para \(t=1,...n\) e \(P=P'-R_{0}\), então podemos reescrever a Equação 4.1 da seguinte forma
\[ \begin{align} P&=R\sum_{t=1}^{n}\frac{1}{(1+i)^t}\\ &=R\left[a^1+a^2+\cdots+a^n\right] \end{align} \tag{4.2}\]
em que \(a=(1+i)^{-1}\). Note que temos uma soma em que cada termo, \(a^t\), é o seu antecedente multiplicado por uma constante \(a\). Denotando \(S_{n}=a^1+a^2+\cdots+a^n\) como a soma dos \(n\) primeiros termos da sequência \(\left(a_{k}\right)_{k=1}^{\infty}\), então é possível escrever cada termo pela diferença de somas sucessivas. Operando algebricamente essa diferença tem-se
\[ \begin{align} S_{n}-S_{n-1}&=a^n \,\,\,\,\, \text{(multiplicando por $a$)}\\ aS_{n}-aS_{n-1}&=a^{n+1} \,\,\,\,\, \text{(subtraindo por $a$)}\\ aS_{n}-\underbrace{a(S_{n-1}+1)}_{S_n}&=a^{n+1}-a\\ aS_{n}-S_{n}&=a(a^{n}-1)\\ S_{n}&=\frac{a(a^{n}-1)}{a-1}. \end{align} \tag{4.3}\]
Logo, a Equação 4.3 descreve uma fórmula fechada para \(S_{n}\). Substituindo a expressão de \(S_{n}\) da Equação 4.3 na Equação 4.2 e reescrevendo \(a\) em termos de \(i\), chega-se a expressão do principal \(P\), dada na Equação 4.4. Esta equação contempla a forma da série uniforme antecipada caso \(R_{0}>0\) e da série uniforme postecipada caso \(R_{0}=0\) (\(P=P'\)).
\[ \begin{align} P&=R_{0}+R\cdot\frac{(1+i)^n-1}{i\cdot(1+i)^n}=R_{0}+R\cdot q_{i,n}\\ P'&=R\cdot q_{i,n} \end{align} \tag{4.4}\]
Repare que \(S_{n}\) é a soma dos \(n\) primeiros de termos de uma sequência em progressão geométrica (PG). Portanto, encontramos a fórmula da soma de uma PG. Baseado nisso, o valor da parcela quando temos as demais variáveis é obtido quando multiplicamos ambos os lado da Equação 4.4 pelo inverso de \(q_{i,n}\). A expressão para encontrar a quantidade de períodos \(n\) a partir das demais variáveis é da forma \[ n = \Biggl\lceil \frac{\log(R)-\log(R-P'\cdot\log(1+i))}{\log(1+i)}\Biggr\rceil. \] Pelo fato de estarmos lidando com períodos, geralmente assumimos como números inteiros. Contudo, não temos garantia que o resultado da fração da equação acima resulte em um valor inteiro. O símbolo representa a função ceiling, que arredonda as casas decimais para o maior inteiro próximo e é definido por \(\lceil a \rceil=\min \big\{ k \in\mathbb{Z} : k \geq a \big\}\). Esse arredondamento ocorre porque em sua grande maioria a capitalização efetivamente só ocorre ao final de cada período inteiro. Desta forma, para ilustrar considere uma aplicação recém lançada que remunera mensalmente. O saldo da conta no início do terceiro mês 3.1 é o mesmo na metade 3.5 e permanece assim até um instante bem próximo 3.95. só sendo efetivamente pago no instante 4.0.
Ampliando a abordagem também para as séries diferidas, com \(m>0\) períodos, podemos generalizar em uma expressão as 3 formas de séries uniformes. Ela é descrita pela Equação 4.5.
\[ \begin{align} P&=R_{0}+R\cdot\frac{(1+i)^n-1}{i\cdot(1+i)^{n+m-1}},\\ P'&=R\cdot q_{i,n,m_1}. \end{align} \tag{4.5}\]
Exemplo 4.1 Presuntinho está pensando em comprar um novo carro. Ele recebeu duas propostas de financeiras distintas, doravante \(\Omega\) e \(\Psi\). A financeira \(\Omega\) propôs duas parcelas iguais de \(50\) mil, sendo a primeira de entrada e a segunda depois de um ano. A \(\Psi\) oferece o financiamento em 24 parcelas mensais iguais de \(5\) mil sem entrada. Presuntinho possui uma linha de crédito no seu banco com juros de 2% a.m. Indeciso ele recorre ao seu consultor financeiro. Na condição de consultor do Presuntinho, qual das alternativas seria mais interessante e por quê?
Na financeira \(\Omega\) temos: \(R_{0}= 50\), \(R= 50\), \(n=2\), \(m=0\) e \(i=0.02\) a.m. \(P_{\Omega} = ?\) Já na financeira \(\Psi\) temos: \(R_{0}= 0\), \(R= 5\), \(n=24\), \(m=0\) e \(i=0.02\) a.m. \(P_{\Psi} = ?\)
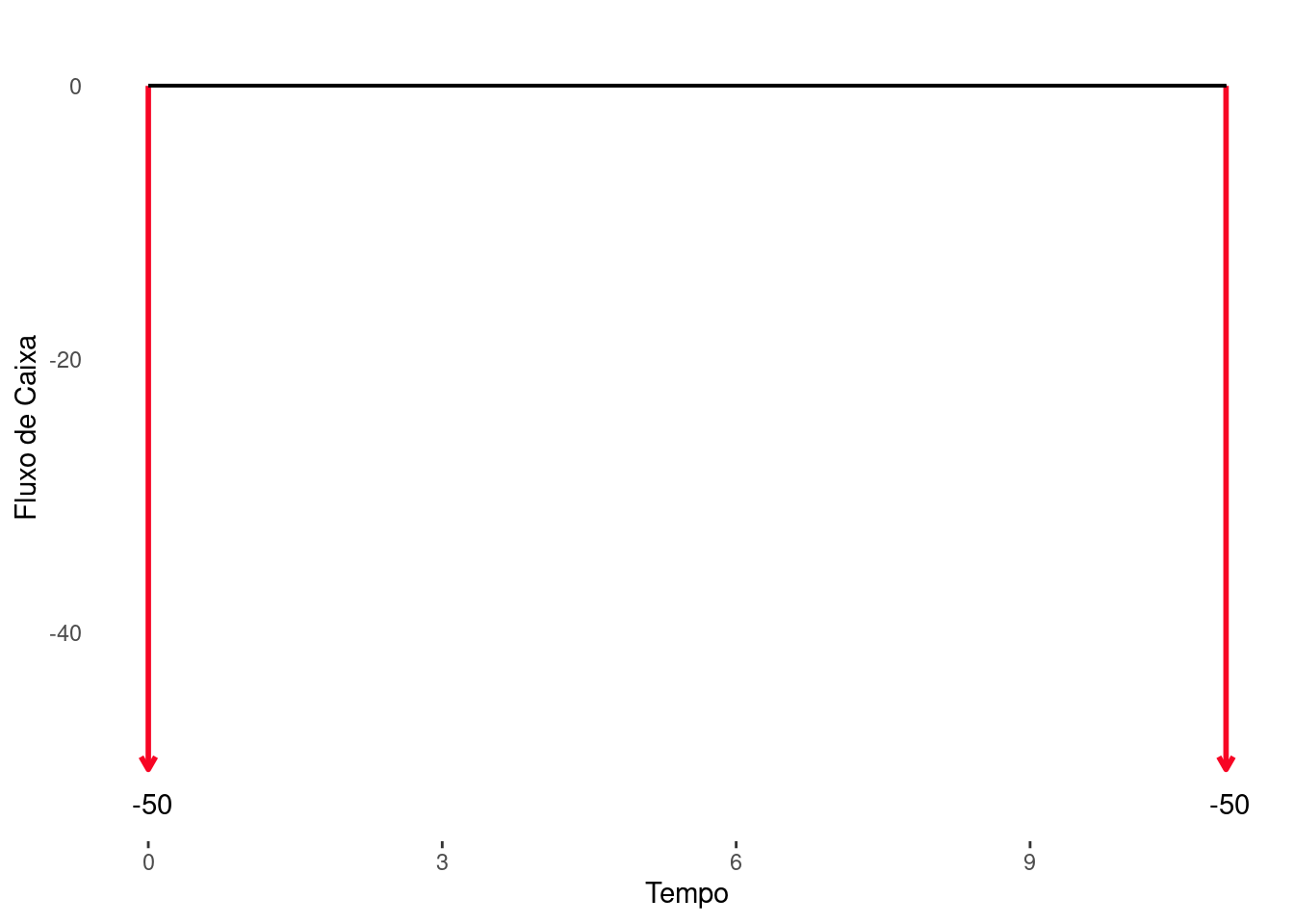
O valor do carro a prazo pela \(\Omega\) é contabilizado seguindo a Figura 4.2. Assim,
\[ \begin{align} P_{\Omega} &= 50+\frac{50}{(1+0.02)^{12}}=89424.66. \end{align} \]
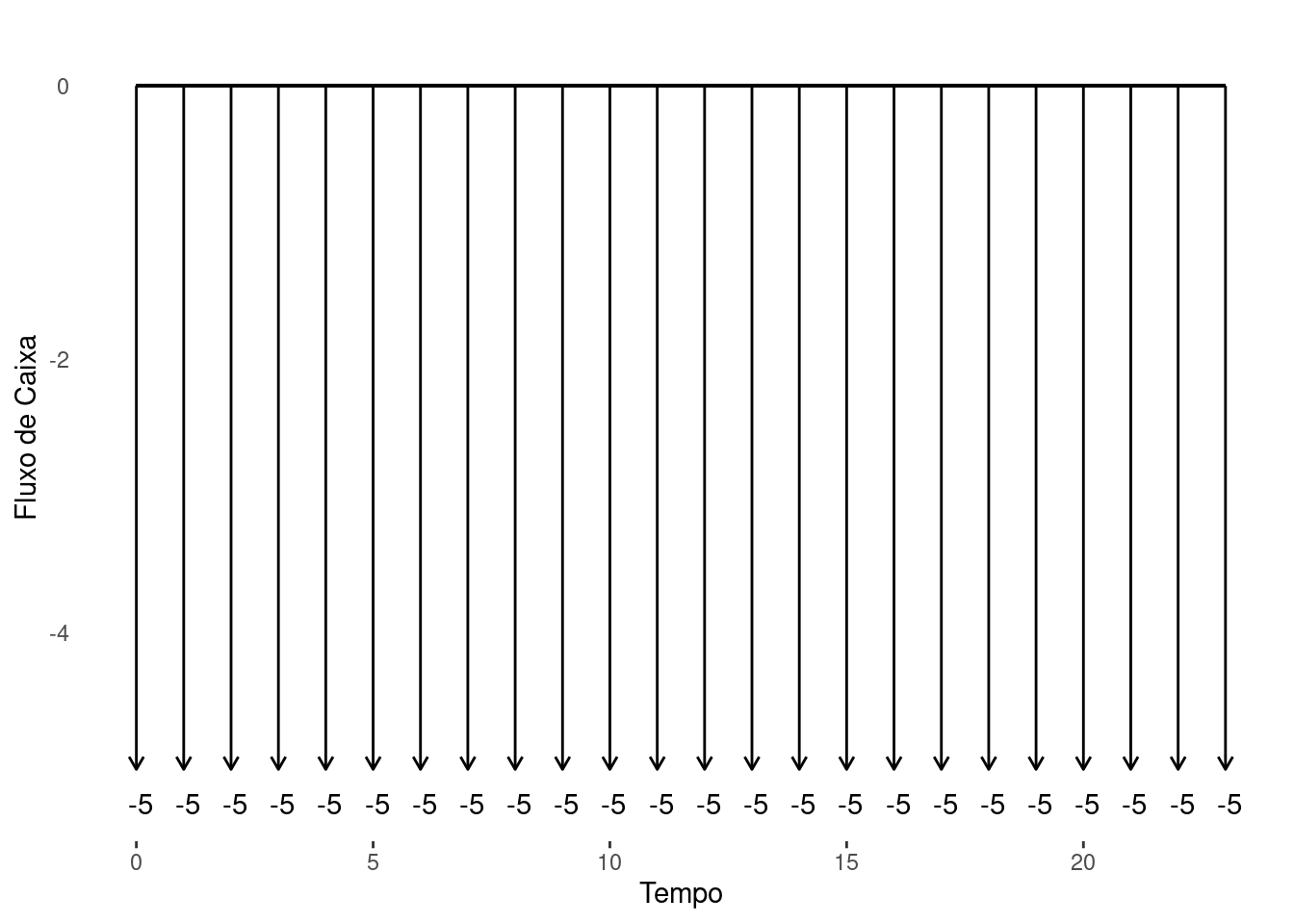
O valor do carro a prazo pela \(\Psi\) é contabilizado seguindo a Figura 4.3. Aplicando a Equação 4.5, computamos o correspondente preço à vista, \(P_{\Psi}\).
\[ \begin{align} P_{\Psi} &= 5\cdot\sum_{t=1}^{24}\frac{1}{(1+0.02)^{t}}\\ &=5\cdot\frac{(1+0.02)^{24}-1}{0.02\cdot(1+0.02)^{24}}=94569.63. \end{align} \]
Como \(P_{\Omega}<P_{\Psi}\), a indicação ao cliente presuntinho seria adquirir o carro pela financeira \(\Omega\), pois levaria a uma economia de \(5144.97\), tomando como base a taxa de juros de 2% de sua linha de crédito.
Primeiramente, zeramos os registros da memória por meio de 
.
Para \(\Omega\) definimos a taxa de juros anual com 1.02 
12 
o que resulta em um juros anual de 26.824%. A partir disso inserimos os inputs: prestação 50 
, o juros anual de 26.824 
e o número de parcelas 5 
e definimos como série antecipadas 
. O output de interesse é o valor presente da \(\Omega\), \(PV_{\Omega}\), ou principal que aqui corresponde ao preço à vista 
. O resultado exibido no display é o preço à vista de 89424.66.
Para \(\Psi\) inserimos os inputs: prestação 5 , o juros de 2 e o número de parcelas 24 . Finalmente, o output desejado corresponde ao preço à vista é calculado pelo o valor presente da \(\Psi\), \(PV_{\Psi}\) ou principal . O resultado final exibido no display é de 64569.63.
Tendo em vista que \(PV_{\Omega}<PV_{\Psi}\), a indicação para cliente presuntinho seria adquirir o carro pela financeira \(\Omega\), já que realizaria uma economia de \(5144.97\) tomando como base a taxa de juros de 2% de sua linha de crédito.
A série uniforme representa majoritariamente a forma de realizar compra e venda a prazo de produtos consumidos em nosso dia a dia. Do ponto de vista prático, a expressão da Equação 4.5 é uma das mais significativas do curso. Nesse sentido, o preço de um produto à vista é representado pelo valor do principal. Do outro lado da equação temos o números de parcelas, \(n\), e taxa de juros \(i\). Com muita frequência nos deparamos com ocasiões em que temos que pagar um valor de entrada \(R_{0}>0\) na compra de uma mercadoria. Com menor frequência, mas ainda sim rotineira, encontramos situações em que a compra de um determinado produto possui um período de carência \(m>0\). Deste modo, é imprescindível compreender sua formulação e saber como utilizá-la. Com base nisso, enunciamos a seguinte regra de bolso (rule of thumb). Muito importante.
Exemplo 4.2 Uma loja financia os móveis planejados para um casal em 4 prestações mensais iguais a R$ 1.300,00 sem entrada. A taxa de juros é de 2.5% a.m. Qual o valor da compra à vista?
Sabemos: \(R_{0}=0\), \(R=1300\), \(n=4\), \(m=0\) e \(i=0.025\) a.m. \(P = ?\).
O valor dos móveis à vista é contabilizado utilizar a Equação 4.5. Assim,
\[ \begin{align} P &= R\cdot\frac{(1+i)^n-1}{i\cdot(1+i)^n}=1300\cdot\frac{(1+0.025)^4-1}{0.025\cdot(1+0.025)^4}\\ &=4890.57. \end{align} \]
Primeiramente, zeramos os registros da memória com .
Na sequência, precisamos inserir os seguintes inputs: prestação 1300 , o valor do juros de 2.5 e o número de parcelas 4 . Output: o valor presente ou principal como o preço à vista .
O resultado final exibido no display é o preço à vista no valor de 4890.57.
A concessão de vendas a prazo impõe alguns desafios aos gestores financeiros ao lidar com as sincronizações de entrada e saída de recursos no caixa. Corporações que possuem um caixa muito folgado adquire menor risco, pois tem capacidade bancar as despesas e custos gerados pelos seus passivos. Por outro lado, uma folga de caixa retém recursos que poderiam ser investido em ativos, por exemplo, envolvendo a atividade fim da empresa. Já as corporações que possuem caixa apertado estão mais expostas a possíveis solvências uma vez que oscilações do mercado ou mesmo uma crise do setor as obriguem recorrer a empréstimos para meramente cumprir com obrigações já acordadas anteriormente e como efeito colateral a alavancar sua estrutura financeira. Contrastando com um caixa mais folgado, essas organizações buscam maximizar seus recursos financeiros nos investimentos da empresa que, em teoria, promoverá no futuro maior capacidade de geração de riqueza ou mesmo em distribuições de dividendos. Todavia, essa posição cobra o custo de perda de liquidez e aumento do risco percebido pelo mercado.
Uma empresa que oferece venda a prazo gera indubitavelmente custos financeiros ao postegar os recebimentos futuros oriundos dos seus clientes. Em outra palavras, ela financia o caixa de seu cliente, uma vez que a diferença dos valores disponíveis em caixa no tempo é ajustado mediante juros. Concomitantemente, a mesma empresa pode obter um financiamento junto aos seus fornecedores ao barganhar maiores prazos para pagamento dos seus insumos e serviços. Para permitir suportar os descasamentos de entrada e saída de caixa, há a necessidade de uma determinada folga, já que o caixa não fica negativo. De maneira genérica, essa folga de caixa é denominada como capital de giro (CG). Como já sabemos, não existe juros zero, logo o capital de giro origina custos financeiros (juros), pois representa um ativo de alta liquidez imobilizado e impossibilitado de ser utilizado para outros fins. Em diversas situações as empresas se valem de sua força econômica e de persuasão de modo a exercer influência sobre os demais agentes do mercado para que possam custear seu capital de giro. Isso lhe permite liberar recursos para serem alocados a outras atividades mais rentáveis e estratégicas.
Neste sentido, considere o exemplo abaixo da empresa do nosso personagem Johnny Cash. Ele planeja realizar uma campanha para alavancar suas vendas. Inevitavelmente a campanha de Cash precisa aumentar o capital de giro e consequentemente incorrerá em custos financeira. É importante notar que apesar da obrigação da existência de tais custos, o agente que financiará não precisa ser o mesmo. Utilizando-se das práticas de mercado e de suas estratégias e artifícios, talvez Cash consiga prospectar outro agente para patrocinar o aumento dos custos financeiros. Por meio do exemplo Exemplo 4.2, abordamos o problema sob a ótica de um consumidor genérico de produtos ou serviços representado na figura do casal. Já no Exemplo 4.3 será do gestor de uma organização representando um fornecedor genérico de produtos ou serviços.
Exemplo 4.3 Johnny Cash possui uma loja chamada Ring of Fire. Ao analisar a série histórica de dados, Cash percebe que há uma retração nas receitas no início do ano. Como forma de impulsionar as vendas do seu principal produto, ele planeja lançar uma promoção do tipo compre agora e só comece a pagar daqui a três meses. A promoção irá oferecer pagamento em quatro parcelas iguais na sua publicidade. O principal produto é um cristal lapidado denominado June Carter. A venda de June Carter responde por 90% do faturamento, onde cada unidade é vendida a 680, fora da promoção. Cash sabe que este tipo de estratégia requer capital de giro (CG) para operar. No entanto, no início do ano a margem do caixa fica extremamente apertada. Sendo assim, haverá necessidade de financiar o CG adicional. Para a linha de crédito de CG, o banco da loja cobra uma taxa de juros de 2.4% a.m.. Ao escrever o material publicitário, Cash fica em dúvida nos valores, mas tem uma certeza, ele não bancará os custos de financiar o CG. Diante deste cenário, preencha o seguinte trecho do material publicitário de acordo com as hipóteses abaixo.
- Cash mantém o preço original e repassa diretamente os juros aos seus clientes.
… Promoção da 💍 Ring of Fire 🔥 de fim de ano! Compre um June Carter em 4 vezes de . Isso não é tudo! Leve agora e só comece a pagar em abril. Pagamento à vista sai no valor de . 🔎 Incidência de de juros nas compras a prazo. Promoção válida somente até 31 de janeiro. 🔎
- Cash reajusta o preço original de forma a repassar indiretamente os juros aos seus clientes.
… Promoção da 💍 Ring of Fire 🔥 de fim de ano! Compre um June Carter em 4 vezes de sem juros. Isso não é tudo! Leve agora e só comece a pagar em abril. Pagamento à vista tem desconto de . 🔎 Promoção válida somente até 31 de janeiro. 🔎
- Cash mantém o preço original e repassa indiretamente os juros aos seus clientes mediante cobrança de custos e tarifas financeiras
… Promoção da 💍 Ring of Fire 🔥 de fim de ano! Compre um June Carter em 4 vezes de sem juros. Isso não é tudo! Leve agora e só comece a pagar em abril. Pagamento à vista sai no valor de . 🔎 Incidência de de tx. abertura de crédito (TAC) nas compras a prazo. Promoção válida somente até 31 de janeiro. 🔎
Concentre nos trechos destacados em negrito no enunciado e utilize a regra de bolso Tip 4.1.
Tendo em mente que Cash não vai absolver os gastos com empréstimos de capital de giro, então outro agente deverá bancar obrigatoriamente. A estratégia, portanto, é utilizar da denominada Psicologia Econômica para estimular as vendas aos seus clientes e paralelamente fazer com que os próprios clientes arquem com os custos financeiros de seus caixas. Uma maneira de compreender esse processo, sem recorrer aos elementos da Psicologia Econômica, é pensar na mecânica contábil em que a cada venda a prazo no valor \(E+J\) que a Ring of Fire realizar em janeiro, ela obtém junto ao banco um empréstimo no valor de \(E\), que corresponde ao mesmo valor de uma venda à vista. Ao entrar no caixa o recurso do empréstimo na mesma quantia do preço à vista, motivada pela venda a prazo ao preço \(E+J\), cria-se um efeito equivalente de uma venda normal com pagamento imediato no caixa da empresa ao preço \(E\). Com o recurso \(E\) disponível na conta da empresa, há um aumento ou manutenção na sua capacidade para bancar as despesas de seus passivos. Transcorrido algum tempo, a Ring of Fire terá de devolver o montante do empréstimo contraído acrescido dos juros (\(E+J\)). O pagamento ao credor exigirá por sua vez saída de caixa, e uma consequente diminuição na sua capacidade de custear as despesas de seus passivos. Imagine que neste mesmo momento de saída de caixa (sincronia), o cliente que outrora havia comprado a prazo, no qual deu origem ao empréstimo, realize o pagamento do produto no valor de \(E+J\). Esta quantia é precisamente o valor liquidado com o banco em razão do empréstimo. A Figura 4.4 mostra de forma ilustrativas esta sequência de operações no caixa ao longo do tempo. Em síntese, o saldo de caixa dessa operação é de \(E\), justamente o valor de uma venda à vista. Surpreso? Por esta razão, a mecânica de contração de dívida casada com a venda a prazo cria um efeito de venda à vista.
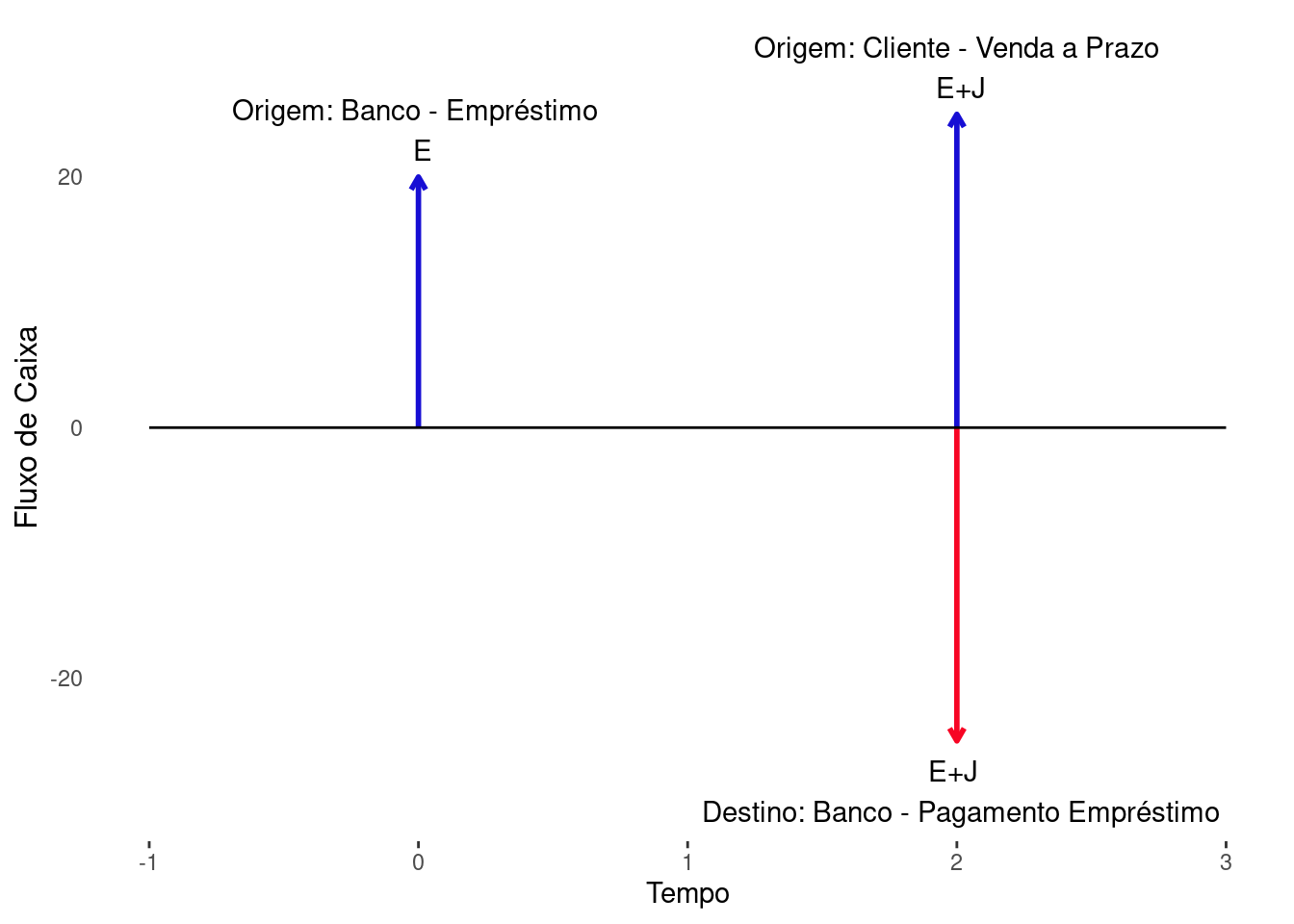
Na hipótese de manter o preço original \(P_{O}\) de 680, os clientes que comprarem a prazo terão que incorrer em parcelas no valor de \(D\), tal que remunere uma venda à vista acrescida dos juros do período. Utilizando a linha de crédito para capital de giro com taxa de 2.4% a.m. obtêm-se uma parcela no valor de 189.08. Isto deve ocorrer para que o valor presente das prestações seja equivalente ao preço à vista de 680, o que corresponde ao preço original.
\[ \begin{align} P_{O}&= \sum_{t=1}^{4}\frac{D}{(1+i_{CG})^{3-1+t}}= \frac{D}{(1+i_{CG})^{2}} \sum_{t=1}^{4}\frac{1}{(1+i_{CG})^{t}}\\ &=D\cdot\underbrace{\frac{(1+i_{CG})^{4}-1}{i_{CG}\cdot(1+i_{CG})^{6}}}_{\text{Função de: } i_{CG}K_{CG}(i_{CG})}=D\cdot K_{CG}(i_{CG})\\ &=D\cdot\frac{(1+0.024)^{4}-1}{0.024\cdot(1+0.024)^{6}}=D\cdot K_{CG}(0.024)\\ &\Rightarrow D =\frac{P_{O}}{K_{CG}}=\frac{680}{3.6}=189.08. \end{align} \tag{4.6}\]
Considerando as práticas e artifícios do comércio e de bancos para remanejar os juros, Cash rearranja os valores de sua publicidade para repassar os juros de forma indireta. Deste modo, ao invés de explicitar os juros para quem não opte pelo pagamento à vista, como na primeira hipótese, ele embute os juros \(J\) ao preço original \(P_{O}\) e tem agora um novo valor para o preço de anúncio \(P_{J}\) (\(P_{J}=P_{O}+J\)). Neste momento, há duas formas de pagamento: a prazo e à vista. Na possibilidade do cliente optar pelo pagamento a prazo, não haverá necessidade de alterar o preço, sendo que já está embutido os juros. Do ponto de vista do cliente, ao multiplicar o número de parcelas pelo valor da prestação, o cliente encontrará o preço de anúncio do produto. Sendo assim, sob a ótica de um consumidor médio, não há incidência de juros (“juros zero”).
Outra forma possível, ocorre quando o cliente opta pelo pagamento à vista. Na eventualidade do cliente não barganhar nenhum “desconto”, \(d_{0}=0\), o pagamento da venda é realizada de imediato, porém ao preço de \(P_{J}=P_{J}-d_{0}\). Isto é, há um acréscimo na margem do produto uma vez que \(P_{J}>P_{O}\). Caso o cliente busque barganhar um “desconto” em razão do pagamento imediato, o vendedor poderá conceder um abatimento máximo de \(d_{max}=P_{J}-P_{O}=J\). Para melhor ilustrar o caso, suponha um produto com preço base de 680 e de anúncio com o valor dos juros embutido de 720. Se no momento da negociação o cliente, que desconhece o preço base, aceitar digamos o “desconto” de 4%, \(d_{sell}\), a venda é concluída com pagamento imediato de 692. Neste caso houve também um aumento da margem original, pois como sabemos \(d_{0}<d_{sell}<d_{max}\).
Pela Equação 4.6 as parcelas de 189.08 durante 4 meses e com 3 meses de carência trazida a valor presente é igual ao preço original. Em função disso, o preço de anúncio que mimetiza um financiamento em 4 vezes “sem juros” e simultaneamente se equipare ao preço original a valor presente é \(P_{B}=756.32 =4\times 189.08\).
\[ \begin{align} d'_{max}&=1-\frac{P_{O}}{P_{B}}=1-\frac{680}{756.32}=0.1\\ d_{max} &=P_{B}\cdot d'_{max}= 756.32\cdot 0.1 = 75.63. \end{align} \tag{4.7}\]
Nas vendas à vista, um vendedor da loja Ring of Fire possui como margem de negociação de “desconto” valores que vão de zero a \(d'_{max}\). No entanto, a concessão do desconto deve obrigatoriamente ser imediata se expresso em publicidade. O valor do desconto máximo em percentuais \(d'_{max}\) bem como em valor absoluto \(d_{max}\) é dado pela Equação 4.7. Em todo caso, a retórica de venda e persuasão se dá em bases de concessão de “desconto” em oposição a uma “penalização” com cobranças a mais por meio juros.
Esse repasse de juros de forma indireta por meio do preço de anúncio acarreta uma desvantagem mercadológica frente aos concorrentes pois fatalmente produz uma inflação no preço, o que tende de forma geral a um menor volume de vendas. Alternativamente, para contornar esse problema, Cash pode decidir fazer um configuração diferente. Ao invés de embutir no preço de anúncio, ele cria custos, taxas e tarifas e os enxerta com juros. Desta forma, a quantia que antes estava inflando o preço do produto, agora é transferida para estes “custos”. Dos resultados da Equação 4.6 sabemos que as taxas de juros disponível para capital de giro acarreta em parcelas de 189.08, por outro lado, caso não existisse juros, cada parcela seria no valor de 170. Sabemos também denominar o que representa o valor da diferença \(189.08-170\) (juros). Sendo assim, podemos adiantar o recebimento desses juros e denominá-los por outros nomes que não sejam juros. Para estimar o valor desse adiantamento, decompomos a parcela \(D_{0}=D-J\) em termos de \(D\) e \(J\) onde \(D_{0}\) é o valor da parcela sem juros. A partir de \(D_{0}\) aplicamos a Equação 4.6 que por sua vez utilizou-se da Equação 4.5.
\[ \begin{align} P_{O} + TAC & = \sum_{t=1}^{4}\frac{D_{0}}{(1+i_{CG})^{3-1+t}}=\frac{D-J}{(1+i_{CG})^{2}} \sum_{t=1}^{4}\frac{1}{(1+i_{CG})^{t}}\,\,\,\,\, (\text{onde }D_{0}=D-J) \\ &=\left(D-J\right)\cdot\frac{(1+i_{CG})^{4}-1}{i_{CG}\cdot(1+i_{CG})^{6}}=\left(D-J\right)\cdot K_{CG}(i_{GC})\\ &=\underbrace{D\cdot K_{CG}(i_{GC})}_{\text{PV preço original}}+\underbrace{J\cdot K_{CG}(i_{GC})}_{\text{Adiantamento de juros}} \\ &= P_{O}+ J\cdot K_{CG}(i_{GC})\\ &\Rightarrow TAC = J\cdot K_{CG}(i_{GC})=19.08\cdot 3.6 = 68.62\\ \end{align} \tag{4.8}\]
De posse desse valor, Cash pode agora nomear a quantia de adiantamento de juros obtida pela Equação 4.8 como Taxa de Abertura de Crédito (TAC), por exemplo, e retirá-la do preço. Nestas condições, na campanha de publicidade o cristal June Carter é anunciado por 680 à vista ou em 4 vezes sem juros e com carência de 3 meses. Perceba que esse preço de anúncio à vista é bem mais competitivo do que o valor anteriormente calculado de 756.32. Outro fator relevante que desperta a atenção de possíveis consumidores é da possibilidade de realizar a compra parcelada sem ter que pagar juros. No instante em que o cliente optar por fazer a compra a prazo, ele é comunicado da existência de tarifas adicionais, sob a alegação de que a empresa já está operando no limite com financiando “sem juros”. Apenas em razão disso, a empresa se ver compelida a repassar esses “singelos, modestos e diversos” custos, taxas, despesas, tarifas tais como: jurídico, gastos com emissão e envio de boletos denominado lâmina de boleto ou taxa de emissão de boleto (TEC), Taxa de Abertura de Crédito (TAC), tarifa de cadastro (TC), comissão de permanência, seguro por morte, análise de score, etc. Ademais, é alegado ao consumidor que é apenas uma única taxa, paga somente no ato da compra. As alegações prosseguem com a argumentação que a promoção já está acabando e na concorrência o consumidor estaria fazendo mau negócio visto que todo mês ele seria cobrado com juros até a última parcela. Do ponto de vista estritamente financeiro, a desvantagem de canalizar todo o valor dos juros para custos e/ou tarifas embutidas em comparação com o artifício de embutir no preço é a perda das possíveis margens adicionais nas vendas à vista e além de não ter margem para captar aqueles clientes que preferem pagar tudo no ato da compra mediante “desconto”. Uma alternativa encontrada nas práticas de mercado é uma combinação entre o artifício de embutir no preço os juros e o restante canalizar para custos virtuais ou imaginários.
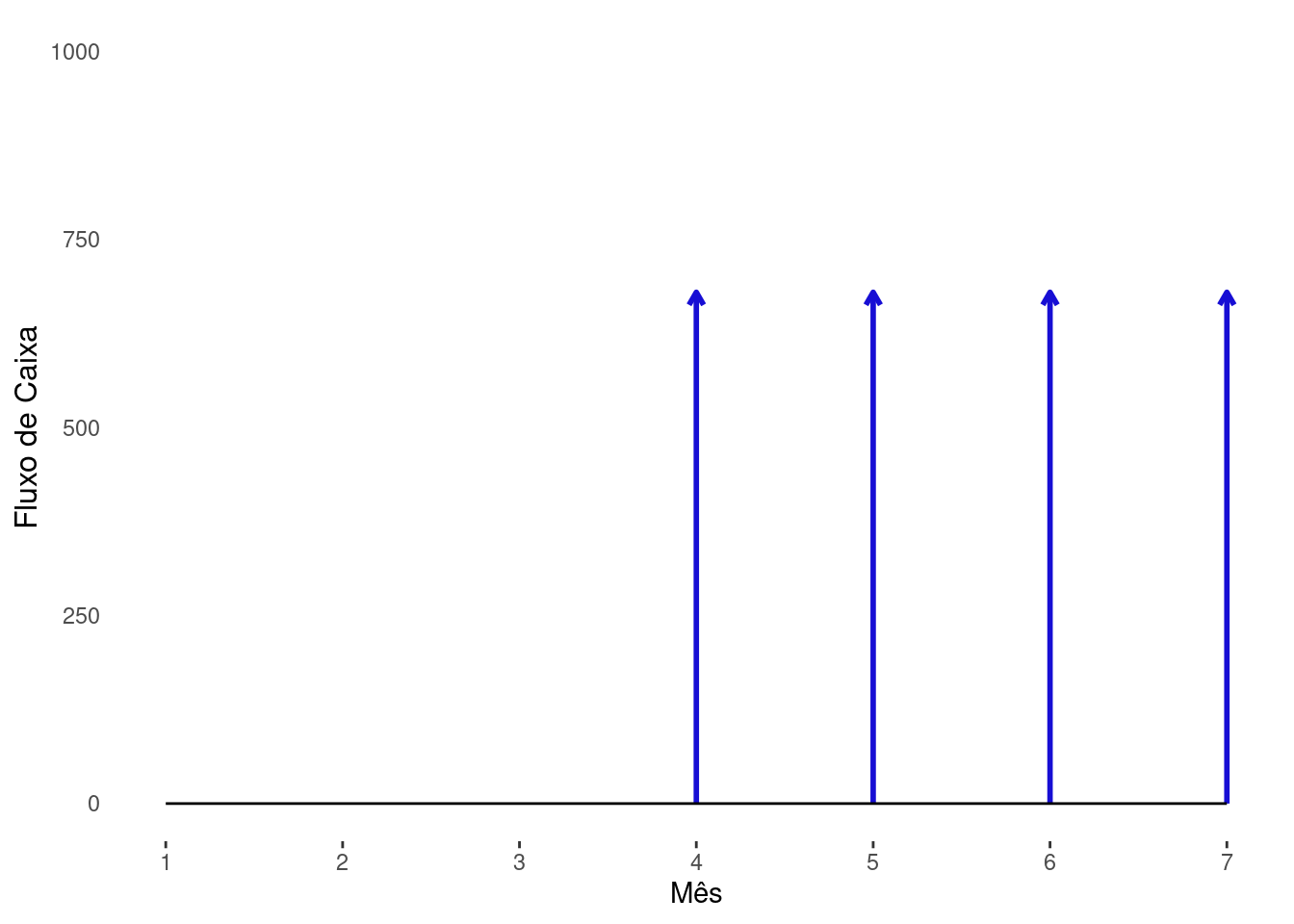
A Figura 4.5 exibe o diagrama de fluxo de caixa para a empresa quando um cliente opte pela compra a prazo. A gestão de caixa requer bom planejamento, em especial na concessão de carência. Uma venda realizada no mês de janeiro só irá começar entrar no caixa da empresa no mês de abril e encerrará somente em julho, isto é, quase metade de um ano. No entanto, outras obrigações operacionais, tributárias e financeiras da empresa continuam demandando recursos do caixa. Em face disto, o capital de giro cumpre um papel fundamental na saúde financeira da empresa. Imagine que nenhuma estratégia de gestão de caixa foi adotada para dar lastro a campanha de alavancagem de vendas. Ademais, vamos admitir ainda que a campanha delineada por Johnny Cash obtenha sucesso absoluto com um aumento significativo nas vendas, sendo todas elas realizadas por meio da promoção. As análises preliminares do desempenho econômico da Ring of Fire serão positivas. Os relatórios irão indicar um crescimento no faturamento, sobretudo na comparação envolvendo sazonalidade, onde já era esperada uma contração das receitas. Outros indicativos também seguirão mostrando a elevação da performance com o aumento de: lucro, retorno sobre o patrimônio líquido (ROE), retorno sobre o ativo (ROA) etc. Entretanto, é importante frisar que mesmo não estando errado está análise, nenhum recurso efetivamente entrou nos cofres da empresa. Esse quadro pode obrigar a organização a ter que recorrer a empréstimos para pagar as contas básicas como salário de funcionários, água, energia, internet, fornecedores etc. Aparentemente contraditório, está é uma situação totalmente plausível de acontecer em virtude da má administração do caixa. Os relatórios de desempenho registram os resultados via regime econômico ou de competência. Em síntese, administrar o caixa de uma empresa é imprescindível para sustentabilidade sendo sua principal ferramenta a matemática financeira.
Repare que todas as 3 hipóteses citadas no Exemplo 4.3 resultam em operações financeiras estritamente iguais. Contudo, na sua opinião, qual das hipóteses levaria a uma campanha publicitária com maior poder de alavancar as vendas? Um consumidor médio consegue perceber essa equivalência?
Nos últimos capítulos lidamos com casos envolvendo títulos de dívidas de empresas ou de países. Por meio dos instrumentos estudados, vimos como precificar um título de dívida, como uma debênture, em que a remuneração ocorre somente no seu vencimento. As taxas de retornos destes títulos são obtidas pelo deságio entre o valor de face e a quantia paga na compra do ativo. Por conseguinte, um investidor firma uma determinada taxa de juros se permanecer com o título em custódia até o seu vencimento. Esta taxa é conhecida no mercado como yield to maturity. De forma ilustrativa, podemos citar os títulos americanos de dívida conhecido por T-bills (Treasury bill). A Figura 4.6 (a) exibe um exemplo do formato físico de um T-bill em 1969. No mercado brasileiro, os títulos do tesouro prefixados, denotados por LTN (Letra do Tesoura Nacional), também apresentam estas mesmas características.
Há contudo, outras modalidades de títulos no qual os juros são pagos periodicamente ao longo do tempo. Os valores das remunerações dos juros são denominados cupom. Similar ao caso anterior, o principal é resgatado somente no vencimento. A partir dos elementos estudados nesta seção, podemos estender nossa análise para os títulos com cupom, visto que estes ativos podem ser representados por uma série uniforme. A Figura 4.6 (b) exibe um exemplar do título americano T-note de 1976 no qual paga cupons semestrais.
Exemplo 4.4 Para financiar o projeto de expansão para região norte do país, a Cambalacho S.A. captou recursos da ordem de 160 milhões. A operação foi realizada por meio de emissão de 40000 debêntures ao mercado. Cada título paga juros de cupom iguais e no valor de 308 por semestre e vencem em 2 anos. Estime a taxa de juros anual captada nessa operação.
O fluxo de caixa gerado por cada debênture adquirida por credor é descrita abaixo.
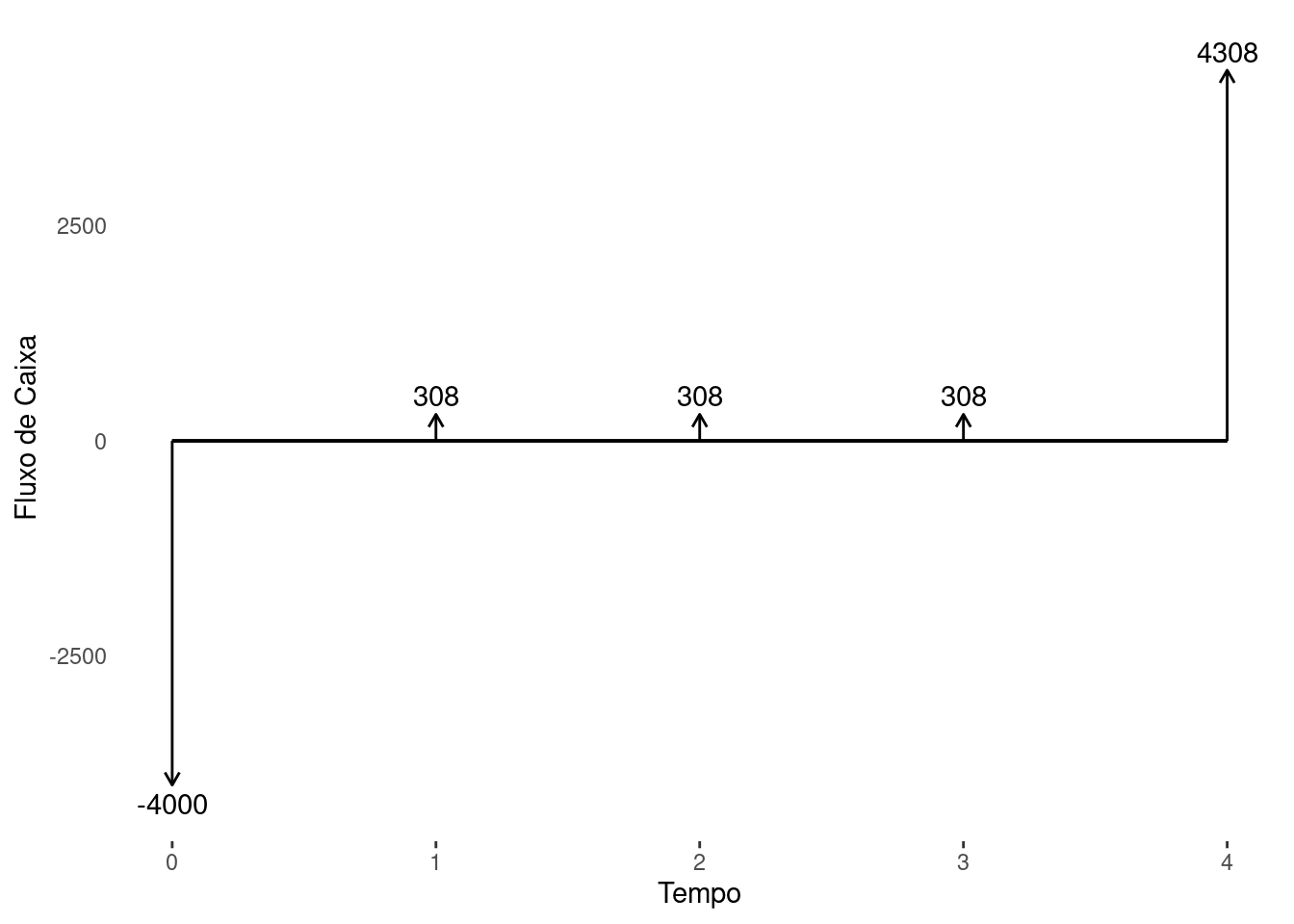
Temos que o \(PV\) da debênture é de \(4000=\frac{160\times10^{6}}{4\times10^{4}}\) e que o cupom é de \(308\) pagos semestralmente. Utilizando a Equação 4.5 encontramos a seguinte função
\[ \newcommand{\argmax}[1]{\underset{#1}{\operatorname{arg}\,\operatorname{max}}\;} \newcommand{\argmin}[1]{\underset{#1}{\operatorname{arg}\,\operatorname{min}}\;} \begin{align} f(i_{s})&=308\cdot\frac{(1+i_{s})^3-1}{i_{s}\cdot(1+i_{s})^3}+\frac{4308}{(1+i_{s})^4}-4000. \end{align} \tag{4.9}\]
A taxa de juros semestral, \(i^{*}_{s}\), é uma raiz da função \(f\). Utilizando operações algébricas usuais não conseguimos achar os valores das raízes. Para encontrá-las precisaremos implementar algum método numérico. Neste caso, utilizaremos a técnica da bisseção por ser um algoritmo de fácil entendimento. A Figura 4.8 descreve os procedimentos passo a passo do método para descobrirmos o valor de \(i^{*}_{s}\) tal que \(f(i^{*}_{s})=0\). Caso não conheça o método da bisseção, uma breve e ótima explicação do algoritmo pode ser acessada clicando aqui. Antes de prosseguir, pare e busque entender o algoritmo e na sequência retome deste ponto.
flowchart LR
subgraph Início
direction TB
A["Def. A0 e B0
L0=[A0, B0]"] --> Z{"Possui Raiz?
f(A0)f(B0)<0"}
Z --> |Não| W["Raiz Não Detectada
no Intervalo
L0=[A0,B0]"]
Z --> |Sim| B["Primeiro Ponto Médio
c #8592; (A0+B0)#8260;2"]
end
Início --> |"Há
Raízes"| C{" Substitui Bk?
f(Ak)f(c)<0"}
C --> |"Sim"| D["Atualização
Bk #8592; c
Ak #8592; Ak"]
C --> |"Não"| E["Atualização
Ak #8592; c
Bk #8592; Bk"]
D --> F["Computa Iteração
k #8592; k+1"]
E --> F
F --> G["Ponto Médio
c #8592; (Ak+Bk)#8260;2"]
G --> H{" Convergência?
|f(c)|<#949;
ou
k>M"}
H --> |Não|C
H --> |Sim|I["Fim
Raiz: c
Iterações: k
Erro: f(c)"]
O primeiro passo é definir um intervalo \(L_{0}=[a_{0},b_{0}]\) onde iremos procurar uma solução da equação de interesse. O segundo passo é averiguar a existência de uma raiz no intervalo \(L_{0}\). A continuidade da função \(f: [a_{0},b_{0}] \mapsto \mathbb{R}\) é a condição necessária, porém não suficiente para permitir postular a existência de uma raiz dentro do intervalo. Adicionalmente, verificando o sinal do produto da função \(f\) avaliada nos dois pontos extremos de \(L_{0}\), \(f(a_{0})\cdot f(b_{0})\), temos um indicativo se há pelo menos uma raiz no intervalo. Caso for positivo, \(f(a_{0})\cdot f(b_{0})>0\), não podemos a priori dizer algo sobre a existência de uma solução no intervalo. Caso for negativo, \(f(a_{0})\cdot f(b_{0})<0\) e aliada a condição de continuidade da função \(f\) em \(L_{0}\), então há pelo menos uma raiz dentro do intervalo \(L_{0}\).
Como estamos trabalhando com uma taxa de juros, então provavelmente não iremos encontrar valores negativos ou valores muito grandes. Consequentemente, podemos supor que o intervalo contendo uma solução da Equação 4.9 deve ser maior que \(0\) e menor que \(0.1\). Contudo, ao observar mais atentamente a Equação 4.9 percebemos que \(i_{s}\neq 0\), pois como todos nós já sabemos, qualquer número dividido por zero é uma indeterminação. Para contornar esse problema, o menor ponto do intervalo é substituído para \(a_{0}=0.0001\). Note que esse novo intervalo é praticamente o mesmo do anterior. O critério de parada do método da bisseção será alcançado quando ocorrer a convergência \(|f(c_{k})|<\epsilon\) ou quando o número de iterações, representado pelo índice \(k=1,2,...\), atingir \(M\). Arbitrariamente definimos \(\epsilon=0.005\) e \(M=100\).
A partir do intervalo definido \(L_{0}=[a_{0},b_{0}]=[0.0001,0.1]\) checamos o sinal do produto \[ f(0.1)\cdot f(10^{-4})=-242.45\cdot 1302.064<0, \] o que indica a presença de pelo menos uma solução dentro do intervalo \(L_{0}\). Pelo fato da função \(f\) ser contínua no intervalo, então existe em \(L_{0}\) ao menos uma raiz real. O terceiro passo é encontrar o ponto médio \(c\) através de \(0.05=(10^{-4}+0.1)/2\). No quarto passo checa-se a convergência \(|f(0.05)|=382.96>\epsilon\). Já que não houve convergência no passo anterior, seguimos para o quinto passo para definir o novo intervalo. Como \[ f(c)\cdot f(b_{0})=f(0.05)\cdot f(0.1)<0, \] então \(L_{1}=[c,b_{0}]=[0.05,0.1]\). De posse do novo intervalo \(L_{1}\), repete-se novamente o processo de forma similar ao apresentado no Diagrama 4.8. A Tabela 4.1 mostra o resultado das demais iterações até atingir o critério de convergência.
| Iteração \(k\) | \(f(c_{k})\) | \(L_{k}\) | \(c_{k+1}\) | \(|f(c_{k})|<\epsilon\) |
|---|---|---|---|---|
| 0 | (0,0.1] | 0.05 | Não | |
| 1 | 382.9627 | [0.05,0.1] | 0.075 | Não |
| 2 | 26.7946 | [0.075,0.1] | 0.0875 | Não |
| 3 | -136.7946 | [0.075,0.0875] | 0.08125 | Não |
| 4 | -56.14985 | [0.075,0.08125] | 0.0781 | Não |
| 5 | -14.6352 | [0.075,0.0781] | 0.07655 | Não |
| 6 | 6.0079 | [0.07655,0.0781] | 0.077325 | Não |
| 7 | -4.3315 | [0.07655,0.07732] | 0.076935 | Não |
| 8 | 0.867 | [0.076935,0.07732] | 0.0771275 | Não |
| 9 | -1.700042 | [0.076935,0.0771275] | 0.07703 | Não |
| 10 | -0.4001 | [0.076935,0.07703] | 0.0769825 | Não |
| 11 | 0.2334 | [0.0769825,0.07703] | 0.07700625 | Não |
| 12 | -0.08335796 | [0.0769825,0.07700625] | 0.07699438 | Não |
| 13 | 0.07495747 | [0.07699438,0.07700625] | 0.07700031 | Não |
| 14 | -0.00413461 | [0.07699438,0.07700031] | 0.07699734 | Sim |
O valor de \(i^{*}_{s}=0.077\) gerado na iteração \(k=14\) corresponde a solução bem aproximada da Equação 4.9 (\(f(i^{*}_{s})=f(0.077)=0\)). Por fim, a taxa de juros \(i\) anual é computada a partir da taxa semestral por
\[ i=(1+i_{s})^{2}-1=0.16. \]
Portanto, a taxa captada pela empresa para financiar sua expansão foi de 16.00% ao ano.
Primeiramente, zeramos os registros da memória com .
Primeiramente precisamos montar os fluxos de caixa do ativo. Inserindo os dados temos: o valor pago pelo título 4000 
, os valores dos cupons 308 3 
(\(308\times3\)) e ao final o valor do cupom adicionado ao principal 4308 . Para a Hp12c iniciar as rotinas numéricas para encontrar a solução digitamos 
. A solução encontrada é 7.7% a.s. Transformando em taxa anual resulta em \(i=0.16\). A taxa captada pela empresa para financiar sua expansão foi de 16.00% ao ano.
4.2 Séries Uniformes Infinitas
As séries infinitas, também conhecidas por perpetuidades ou séries perpétuas, são aquelas que as transações de entrada e saída de caixa se estendem ad eternum. Exemplos de séries perpétuas podem ser observados em planos de aposentadoria complementar que geram uma renda vitalícia. Elas também podem ser vistas em títulos corporativos como os consols ingleses, em que são pagos cupons eternamente (Bruni e Famá 2012).
A Equação 4.5 nos permite calcular a série de um número finito de pagamentos ou recebimentos \(n<\infty\). Para estender o caso para uma série infinita de transações \(R\) necessitamos avaliar o limite da série quando \(n\) tende ao infinito,
\[ \begin{align} PV=\sum_{t=1}^{\infty}\frac{R}{(1+i)^t} &= \lim_{n\rightarrow\infty}\sum_{t=1}^{n}\frac{R}{(1+i)^t} = \lim_{n\rightarrow\infty}\frac{R\cdot(1+i)^n-1}{i\cdot(1+i)^n} \\ &= \lim_{n\rightarrow\infty}\frac{R\cdot(1+i)^n}{i\cdot(1+i)^n}-\lim_{n\rightarrow\infty}\frac{R}{i\cdot(1+i)^n}\,\,\,\,\text{ (Limite da soma é a soma dos limites) }\\ &=\frac{R}{i}-\frac{R}{i}\cdot\lim_{n\rightarrow\infty}\frac{1}{(1+i)^n}\,\,\,\,\text{ para }\,\,i>0 \\ &=\frac{R}{i}+0. \end{align} \]
A expressão \(PV\) da equação acima é a resultante da soma das infinitas transações trazidas a valor presente por uma taxa de desconto \(i\). A fórmula do valor presente de séries perpétuas, onde não há crescimento, é dada por
\[ \begin{align} PV &= \frac{R}{i}. \end{align} \tag{4.10}\]
A Equação 4.10 considera as transações do fluxo de caixa sempre homogêneas e com crescimento zero. Suponha que a série perpétua tenha um fluxos de caixa com taxa de crescimento constante \(g\) ao longo do tempo. Sendo assim, a transação de cada período é computada por \(R_{t}=R_{0}\cdot(1+g)^t=R_{1}\cdot(1+g)^{t-1}\) onde \(g<i\). Por conseguinte,
\[ \begin{align} PV &=\sum_{t=1}^{\infty}\frac{R_{t}}{(1+i)^t} = \sum_{t=1}^{\infty} \frac{R_{0}(1+g)^{t}}{(1+i)^{t}}\\ &=\sum_{t=1}^{\infty} \frac{R_{1}(1+g)^{t-1}}{(1+i)^{t}} =\frac{R_{1}}{(1+i)}\cdot\sum_{t=1}^{\infty} \left(\frac{1+g}{1+i}\right)^{1-t}\\ &=\frac{R_{1}}{(1+i)}\cdot \frac{1}{1-\frac{1+g}{1+i}} =\frac{R_{1}}{(1+i)}\cdot \frac{1}{\frac{1+i-1-g}{1+i}} \\ &=\frac{R_{1}}{i-g}. \end{align} \tag{4.11}\]
A expressão da equação acima generaliza a Equação 4.10 e foi apresentada por Gordon e Shapiro (1956), inspirados no trabalho Williams (1938). Usualmente a Equação 4.11 é conhecida como Modelo de Crescimento de Gordon ou simplesmente Modelo de Gordon, onde \(R_{t}\) é o provento gerado pelo dividendo distribuído pela empresa no tempo \(t\), \(g\) a taxa de crescimento dos pagamentos de dividendos e \(i\) é o custo de capital ou o retorno esperado. A precificação de um ativo via Equação 4.11 se ampara na ideia do ativo de refletir o valor presente do fluxo de caixa de todos seus dividendos futuros (Ross, Westerfield, e Jaffe 2012).
Os artifícios e meandros praticados no mercado pelo comércio e por instituições financeiras abordadas no Exemplo 4.3 e em exercícios deste capítulo são de caráter meramente educativos. A análise concentra-se na fundamentação financeira e econômica. Por meio delas examinamos como alguns artifícios podem ou devem ser interpretados e seus efeitos a luz da matemática financeira, que perpassa a dimensão territorial e temporal. Desta forma, o estudo sobre o objeto não está circunscrito ao ordenamento jurídico a menos pela prática efetiva do próprio objeto, os quais sim estão sujeitos a determinação de sua localidade, tempo e sendo passíveis de penalidade.
Em suma, não há aqui qualquer endosso as práticas e artifícios que foram objetos de análise. Ressalta-se ainda que mesmo sendo alguns artifícios legais e corriqueiros seus objetivos não são nada munificentes, e em certas circunstâncias questionados ao menos do ponto de vista ético. Se tratando de práticas no âmbito brasileiro, a cobrança, por exemplo, de Taxa de Abertura de Crédito (TAC) e Tarifa de Emissão de Carnê (TEC) são práticas ilegais uma vez que não constam listadas na resolução do BACEN CMN 3919/2010 e já respaldada em jurisprudência, sendo matéria do acórdão 1176340. Por fim, no entendimento do autor, o caminho para emancipação da sociedade passa irremediavelmente pelo conhecimento.
4.3 Exercícios
Exercício 4.1 O vendedor de uma empresa concorrente ao da Loja tratada no Exemplo 4.2 propõe para o casal os mesmos móveis em 4 prestações mensais iguais sem juros a fim de cobrir a oferta da concorrência. Na proposta cada parcela fica em R$ 1.222,65 (\(4 \times 1222.65=4890.60\)). O casal decide então aceitar a oferta e são encaminhados para o setor financeiro. No ato da assinatura do contrato de compra e venda, eles descobrem que o financeiro repassa alguns custos como: taxa de abertura de crédito, lâmina do boleto, seguro por morte, despesas de correio, taxa de cadastro etc. A alegação do vendedor seria de que a empresa já está financiando sem juros e não poderia arcar com estes gastos adicionais. Os custos requeridos totalizam R$ 320,00. Dino acho justo e fica convencido, porém sua esposa Fran não se convence. Ela começa a se lembrar de suas aulas de Matemática Financeira (MatFin) e diz ao vendedor que iriam pensar, porém se comprometeu a dar uma resposta no dia seguinte. Seu esposo Dino, que nunca fez o curso de MatFin, fica sem entender mas concorda. No lugar da Fran, qual seria sua decisão no dia seguinte e qual a justificativa?
Lembre-se da regra Tip 4.1.
O valor à vista dos móveis de ambas as lojas são praticamente iguais, doravante Loja I e II. Considerando a quantia de R$ 320 como adiantamento das parcelas da Loja I, então
\[ \begin{align} \underbrace{4890}_{\text{à vista}}-\underbrace{320}_{\text{taxas}}&=\left[\underbrace{1222.65}_{\text{parc.}}-\underbrace{A}_{\text{adiantamento}}\right]\cdot\frac{(1+i)^4-1}{i\cdot(1+i)^4}\\ 320&=A\cdot\frac{(1+i)^4-1}{i\cdot(1+i)^4}=A\cdot 3.762\\ \Rightarrow A&=85.06. \end{align} \] Em suma, se utilizarmos os valores dos “custos” da Loja II para adiantar as parcelas, teríamos prestações de R$ 1137.59 (\(1222.65-85.06\)). Em outras palavras, as parcelas da Loja I seriam menores que a Loja II. Portanto, a decisão seria não assinar o contrato. A argumentação se funda a partir da regra de bolso Tip 4.1. Com isso, percebemos facilmente o fato de que os juros estão escondidos nos “custos” alegado pela financeira da Loja II.
Exercício 4.2 Uma pequena rede de lojas tem um projeto de atualizar o sistema de segurança e implementar uma solução integrada entre todas as unidades da rede. O orçamento para realizar o projeto é de 28 mil. Existem duas alternativas disponíveis. A primeira é captar os recursos necessários mediante um empréstimo do banco, no qual possui conta, que cobra uma taxa de 2.6% a.m. para essa linha de crédito. A segunda é aceitar o financiamento da empresa que faz a instalação dos equipamentos de segurança. A empresa de segurança divide o pagamento em 6 parcelas mensais com entrada, no valor de 4950. Qual a melhor alternativa para essa rede de lojas?
Encontre a taxa de juros praticada no financiamento oferecido pela empresa de segurança. Na sequência compare com a taxa de juros da linha de crédito do banco.
Pegar financiamento com a empresa de segurança.
Exercício 4.3 A incorporadora Rock iniciou a entrega das unidades do seu novo empreendimento, o condomínio Bed-Stuy. No lançamento de vendas são oferecidos aos clientes um financiamento em 48 prestações mensais sem entrada iguais de 4500 reais ou alternativamente uma entrada paga no ato e mais 60 parcelas trimestrais no valor de 8600 reais. Sabendo que a taxa de juros praticada no mercado para o financiamento habitacional desse tipo é de 34.5% a.a., calcule o valor da entrada que deverá ser paga.
Ambos os financiamentos devem ser iguais. Isso significa dizer que os fluxos de caixas de ambas alternativas de financiamento tem que corresponder ao mesmo valor presente.
Exercício 4.4 Após a festa da boa vizinhança, o senhor Barriga aquece seu coração e acaba perdoando todas dívidas do seu Madruga. Para evitar topar com o Chaves na Vila e ser recebido com uma pancada, o papai do Nhonho oferece também alguns meses de carência. Porém, após este período o valor do aluguel será ajustado para 500 mangos. Sabendo que cada unidade da Vila vale 43500 mangos, com a exceção da casa 71, quantos meses de carência seu Madruga conseguiu? Considere uma taxa de juros de 1% a.m.
O aluguel de um ativo imobiliário pode ser visto como uma série perpétua de pagamentos. Mediante a taxa de juros e do valor de aluguel podemos definir uma cotação de referência do imóvel.
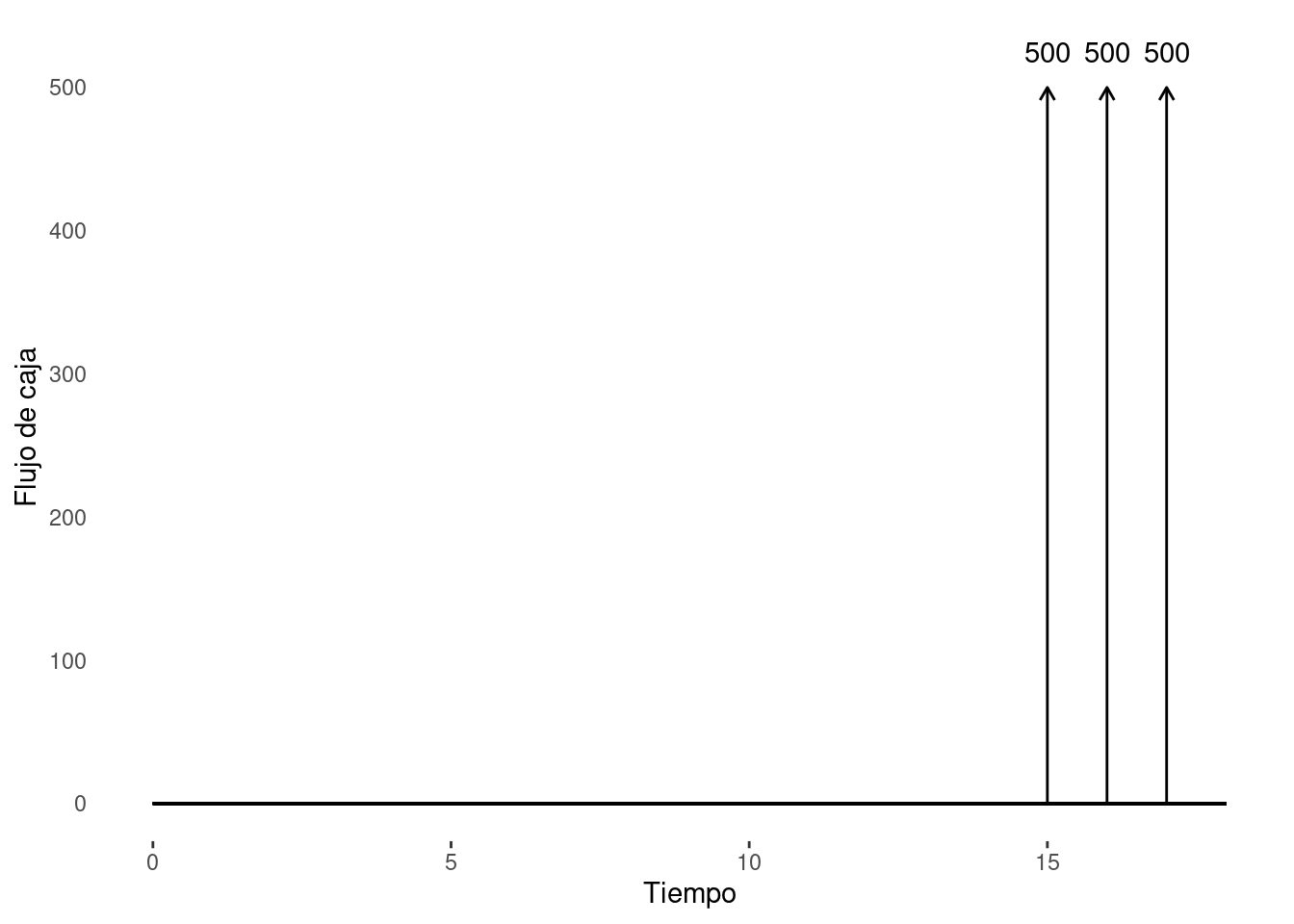
Diagrama Fluxo de Caixa - Senhor Madruga.
Ao final do período de carência de \(m\) meses, irá “iniciar” uma série de pagamentos \(D\) perpétua. Por intermédio da Equação 4.10, sabemos o valor da série no período \(m\). Na sequência, levando essa quantia a valor presente e igualando ao valor do imóvel temos
\[ \begin{align} PVc&=\frac{D/i}{(1+i)^m}\\ 43500 &=\frac{50000}{(1+0.01)^m}\\ 1.01^m&=\frac{500}{435}\\ m\log(1.01)&=\log(1.149425)\\ m&=\frac{\log(1.149425)}{\log(1.01)}\\ m&=14. \end{align} \]
Portanto, o senhor Madruga terá mais 14 meses sem pagar o aluguel. Todavia, durante esse período não será necessário se esconder do senhor Barriga.
Exercício 4.5 Uma loja de carros semi-novos está anunciando numa rádio local a venda de um carro por 62000 sendo 2000 de entrada e 20 parcelas mensais iguais a 3000 “sem juros”. George Box entusiasmado com a propaganda foi até a loja. O vendedor ofereceu um desconto na compra a vista de 8%. Porém, Box preferiu financiar a compra do carro. No momento de realizar o financiamento foi informado que havia taxas para despesas legais para registrar os documentos junto ao banco de 2.5% do valor do automóvel mais uma tarifa fixa de 650. Box está pagando juros? Se sim, qual o valor da taxa de juros?
Lembre-se da regra Tip 4.1.
Sabemos que não existe financiamento sem juros. Ainda que o consumidor não pague os juros, outro agente irá absolver esses valores. Pela regra Tip 4.1 ,temos que encontrar o preço à vista e o não à vista para encontrar os juros. De posse dos dois valores, igualamos os respectivos fluxos de caixa para uma mesma data focal. Geralmente definimos o tempo \(t=0\). A taxa de juros \(i\) é o valor que vai satisfazer a igualdade dos valores de ambos fluxos de caixa.
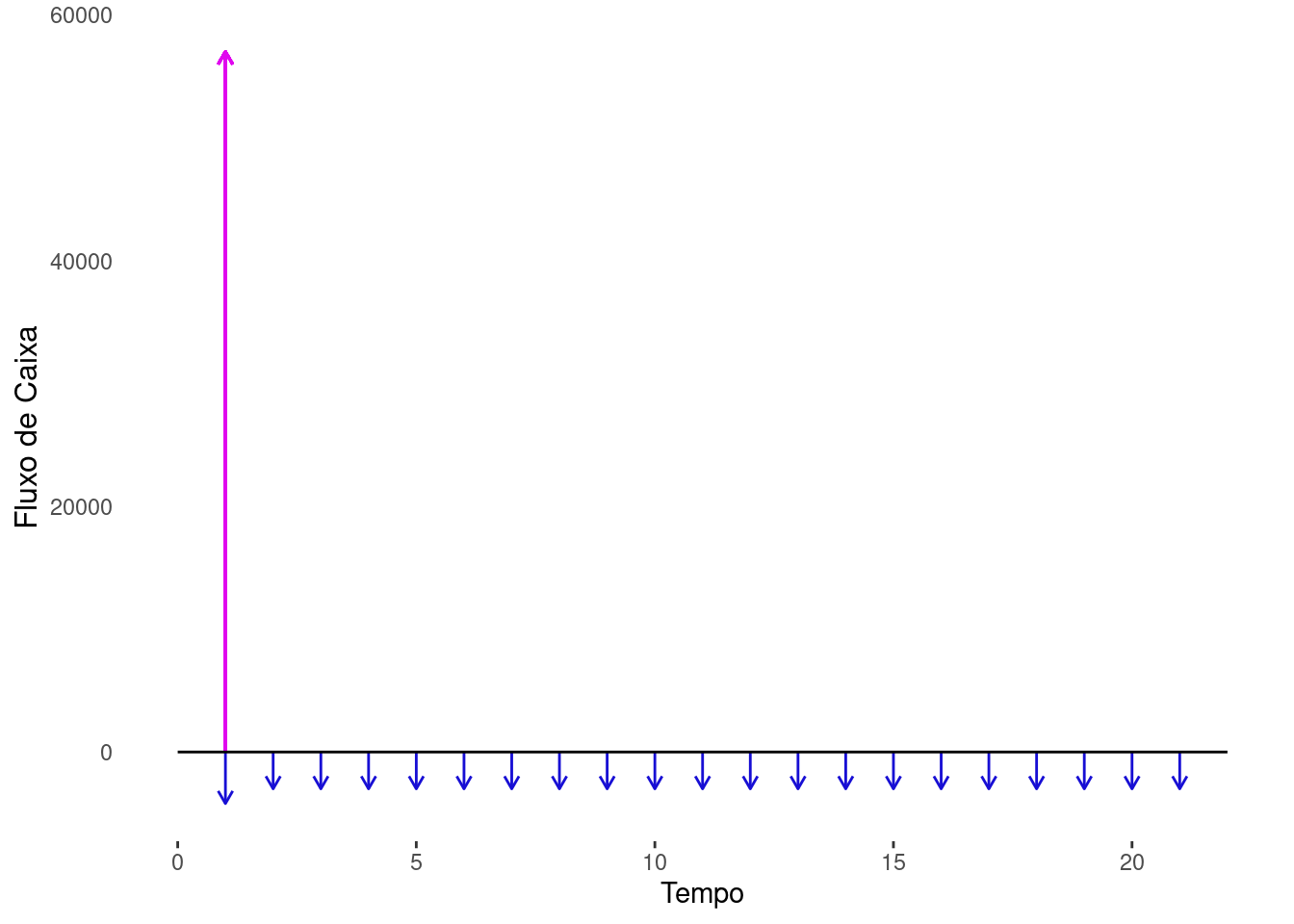
Valor Anunciado - \(V_{x}\): 62000
Valor Financiado - \(V_{fin}\): 60000
Entrada - \(D_{0}\): 2000
Taxa Fin. - \(b_{x}\): 3.5%
Prestações - \(D\): 3000
Tarifa: \(b_{0}\): 650
N. Parcelas - \(n\): 20
\[ \begin{align} \text{Carro}&=\text{Carro}\\ \text{Preço à Vista}&=\text{Fluxo Caixa Não a Vista}\\ 0.92\cdot V_{x} &=V_{x}\cdot b_{x}+b_{0}+D_{0}+ \sum_{t=1}^{n}\frac{D_{t}}{(1+i)^t} \,\,\,\, \text{(Subst pelos valores numéricos)} \\ 0.92\cdot 62000 &= 62000\cdot 0.035+650+2000+3000\cdot\sum_{t=1}^{20}\frac{1}{(1+i)^t}\\ \frac{52220}{3000}&=\sum_{t=1}^{20}\frac{1}{(1+i)^t} \,\,\,\, \text{(Aplicando a fórmula da PG)}\\ 17.04&=\frac{(1+i)^{20}-1}{i\cdot(1+i)^{20}}\\ h(i)&=\frac{(1+i)^{20}-1}{i\cdot(1+i)^{20}}-17.04 \end{align} \]
A taxa de juros que Box incorreu é o valor de \(i^{*}\) tal que \(h(i^{*})=0\). Em outras palavras, \(i^{*}\) é uma raiz da função \(h\). Aplicando algum método numérico para calcular a raiz de função obtemos o valor da taxa de juros de \(i^{*}=0.0136\) ou 1.36% a.m. Para calcular a taxa por meio da hp12c introduzimos como input 52220 20 3000 . Por fim, para estimar a taxa de juros basta digitar . O resultado final é exibido no display.
Exercício 4.6 Hermes, o irmão do Renato, comprou um sofá para sua casa em 4 parcelas mensais constantes (1+3), no valor de 900, com uma entrada. Se tivesse pago a vista, o preço seria de 2611.00 reais. Qual o valor da taxa de juros mensal embutida nessa compra?
Leia a apostila.