3 Regimes de Juros Compostos
Neste capítulo estenderemos as ideias do juros simples discutida no capítulo anterior para construirmos a lógica de operação no regime de juros compostos. Salvo raras exceções, a capitalização composta surge naturalmente nas relações econômicas e é o regime adotado nas práticas cotidianas do mercado. Inicialmente, deduziremos a fórmula geral da evolução do valor futuro \(FV\) de um título em função do tempo dado um montante inicial e uma taxa de juros. Por meio da expressão geral, caracterizaremos o comportamento da curva de crescimento de um ativo governado por regime composto. Para compreendermos melhor, relacionaremos o comportamento da curva gerada por um regime de juros compostos com a do regime simples. Trataremos também o problema inverso, que consiste na redução das grandezas futuras ao serem trazidas para valor presente \(PV\) por meio de desconto em regime composto. A exemplo do capítulo anterior, boa parte dos casos numéricos abordados aqui, as soluções são acompanhadas com o uso da calculadora financeira Hp12c.
3.1 Expressão Geral
Para demonstrar a fórmula que descreve o valor futuro \(FV\), podemos tomar como ponto de partida o caso dos investimentos dos irmãos Pinky e Cérebro no Banco ACME. Neste banco, o regime de juros adotado é simples e oferece papéis de renda fixa com taxa de juros de 10% ao ano. Tanto Pinky quanto Cérebro investiram nesses papéis R$ 5.000,00 inicialmente. No entanto, cada um dos irmãos usou uma estratégia diferente na aplicação financeira. Lembra? Caso não se lembre, revise o exemplo do Banco ACME.
No Capítulo 2 tratamos do caso do Pinky para compreender como calcular o \(FV\) em cada ano considerando um determinado investimento inicial e que ele somente sacou o montante da sua conta no final dos 5 anos. Com base nisso, conseguimos montar uma tabela que descrevia a evolução anual de seus ganhos. A Tabela 3.1 mostra como seria essa mesma evolução para um determinado investimento inicial \(V_{0}\) e uma certa taxa de juros \(i\) anual durante um período de 10 anos. Já neste capítulo focaremos nossa atenção em como ocorre a evolução do montante considerando a estratégia do Cérebro.
Nosso interesse, portanto, corresponde em obter o valor futuro \(FV\) a partir de uma expressão geral. Deste modo, dado um aporte inicial \(V_{0}\) e uma taxa de juros \(i\), poderemos calcular o montante de um investimento em renda fixa para qualquer instante de tempo. Para facilitar o entendimento de como encontrar tal expressão, iremos recorrer ao caso da evolução do investimento do Cérebro ao longo do tempo. Estes valores estão descritos na última coluna da Tabela 3.2. De forma genérica, considere \(n\) o número de período e \(FV_{n}\) o valor futuro após \(n\) períodos. Neste nosso caso, \(n\) é retratado pelo número de anos.
Para o primeiro ano de investimento computamos o saldo final da conta do Cérebro utilizando a Equação 2.2. Como ilustrado no capítulo anterior, isto ocorre porque o banco ACME trabalha com juros simples. Isto posto, ao final do ano (\(n=1\)) o montante total \(FV_{1}\), composto pelo principal \(V_{0}\) e o juros remunerado, é calculado por
\[ \begin{align} FV_{1} & = V_{0} +\text{Juros} = \underbrace{V_{0}}_{\text{Inv. Inicial}} +\underbrace{V_{0}\cdot i}_{\text{Juros}}\\ & = V_{0}(1+i). \end{align} \] Diferentemente de Pinky, após receber os juros, o Cérebro retira todo seu saldo \(FV_{1}\). No início do segundo ano, ele repete o mesmo procedimento, no entanto, investindo agora \(FV_{1}\), isto é, o valor obtido no ano anterior \(n=1\). Por conseguinte, este valor passa a ser seu novo investimento inicial. Assim, o montante acumulado no final do ano \(n=2\) é calculado por
\[ \begin{align} FV_{2} & = \text{Inv. Inicial} + \text{Juros} = \underbrace{FV_{1}}_{\text{Inv. Inicial}} +\underbrace{FV_{1}\cdot i}_{\text{Juros}}\\ & = FV_{1}\cdot(1+i) = V_{0}(1+i)\cdot(1+i) \,\,\,\text{(Lembre-se que } FV_1=V_{0}(1+i)\text{ )}\\ & = V_{0}\cdot(1+i)^2. \end{align} \tag{3.1}\]
Seguindo da mesma forma no terceiro ano (\(n=3\)) e com um investimento inicial de \(FV_{2}\), temos ao final deste ano
\[ \begin{align} FV_{3} & = \text{Inv. Inicial} + \text{Juros} = \underbrace{FV_{2}}_{\text{Inv. Inicial}} +\underbrace{FV_{2}\cdot i}_{\text{Juros}} \\ & = FV_{2}\cdot(1+i) = V_{0}(1+i)^2\cdot (1+i) \,\,\,\text{(Note que } FV_2=V_{0}(1+i)^2\text{ )}\\ & = V_{0}(1+i)^3. \end{align} \]
Perceba que um padrão se estabelece na medida em que vamos encontrando os valores de \(FV_1\), \(FV_2\) e \(FV_3\). As expressões para os valores futuros dos anos \(n=1,2,3\) dependem dos mesmo termos \(V_{0}\) e \(i\). O termo que se altera é somente o expoente de \((1+i)\) e ele sempre é igual ao número de períodos \(n\). Isto ocorre de tal sorte que poderíamos escrever o valor futuro de um dado ano qualquer \(n\), representado por \(FV_{n}\), pela seguinte fórmula \[ FV_{n}=V_{0}(1+i)^n, \tag{3.2}\] onde \(V_{0}\) é o valor investido inicialmente, \(i\) é a taxa de juros constante aplicada a cada período e \(n=0,1,2,3,4,...\). Portanto, a partir da Equação 3.2 temos a descrição do funcionamento dos juros compostos.
Apesar da expressão da Equação 3.2 ao qual encontramos está correta, ainda padece de uma argumentação matemática do porque ela será sempre válida, isto é, para todo \(n\) pertencente aos números naturais \(n\in\mathbb{N}\). Ao final deste capítulo, damos um pouco mais de formalismo para mostrar a validade desta relação através da indução matemática. Apesar de simples a demonstração sua estrutura lógica e argumentativa é extremamente interessante.
Por meio da Equação 3.2 podemos montar a Tabela 3.2. Para isso, basta apenas conhecermos o valor aplicado no instante \(n=0\) e a taxa de juros \(i\) que o banco ACME pratica. A partir da expressão da equação, também já podemos ter em mente o comportamento da curva de crescimento dos montantes no caso do investidor Cérebro. Ao olhar para Equação 3.2 você consegue saber como é esse comportamento? Que diferença deve existir entre esta curva e a correspondente curva representada pelo investimento do Pinky?
Antes de prosseguir, manipule de maneira sutil e gradativa, no painel abaixo, os parâmetros correspondentes ao \(V_{0}\) do Pinky, \(V_{0}\) do Cérebro e a taxa de juros \(i\) anual paga pelo banco ACME. Juntamente com os valores das Tabelas 3.1 e 3.2, confira a representação gráfica das evoluções das respectivas curvas e se elas estão de acordo com o que você esperava.
Na Equação 3.2 a interpretação do termo \(V_{0}\) como um investimento inicial pode ser estendido para um caso mais amplo. Podemos interpretar esse termo como sendo uma dívida ou mesmo o preço de um apartamento na planta. No intuito de ampliar a interpretação para um caso mais generalista, utilizamos o valor presente \(PV\). Consideramos \(n\) como sendo a quantidade de períodos a frente da data presente e \(i\) a taxa de juros que incide em cada período. Portanto, de forma equivalente a Equação 3.2, a expressão geral que descreve o \(FV\) em relação a essas variáveis é dada por
\[ FV=PV(1+i)^n. \tag{3.3}\]
Note que do ponto de vista matemático as equações 3.2 e 3.3 são estritamente equivalentes. A diferença entre as equações reside meramente na interpretação dos termos. No caso do investimento dos personagens Pinky e Cérebro o valor presente \(PV\) é representado pelo valor que os irmão investiram no instante inicial. Em outro caso, o valor presente poderá representar outra quantidade tal como o preço de um eletrodoméstico que um consumidor deseja financiar em uma loja de um shopping.
A Equação 3.3 é uma das equações mais importantes do curso de matemática financeira. Apesar de simples podemos obter várias informações acerca dos ativos financeiros tais como: a projeção futura do montante total de uma dívida gerada por um empréstimo bancário durante um dado intervalo de tempo; a natureza do comportamento da curva de crescimento de uma dívida; qual o valor que deve ser investido hoje em um produto financeiro com objetivo de acumular uma certa quantia no futuro a fim a ser desfrutada em uma viagem ou casamente; na escolha dentre dois investimentos distintos, selecionar qual deles apresentará o menor tempo para alcançar seu correspondente investimento inicial (payback); qual o efeito esperado no valor de um título de dívida se a taxa de juros mudar; qual o decréscimo de uma dívida provocada por um adiantamento parcial do seu montante final. Perceba as inúmeras situações nas quais esta equação está intrinsecamente associada. Em suma, mais do que saber a fórmula, devemos compreender as relações entre as variáveis descritas por meio de sua expressão matemática.
Exemplo 3.1 Um banco de investimento oferece dois produtos financeiros aos seus cliente sendo elas mutualmente excludentes. Nos seus respectivos prospectos consta as seguintes informações:
Fundo de investimento com ativos capitalizado via regime simples com juros de 12% ao ano e um período de vigência de 17 anos. Este fundo não há cobrança de taxas para ingressar.
Fundo de investimento com carteira de ativos capitalizados por regime composto com taxa de juros anual de 10% e um período de 15 anos. O fundo cobra um pedágio de entrada no valor de 4000,00 pago uma única vez.
Um investidor, correntista deste banco de investimento, deseja aplicar 16.000,00 reais. Entretanto, ele encontra-se muito indeciso. Antes de aplicar, esse investidor contrata seus serviços de consultoria financeira. Diante dos dados apresentado responda:
Em sua consultoria, qual dos fundos de investimento você indicaria ao seu cliente?
Caso o tempo de vigência dos fundos se alterem para 10 anos sua indicação de investimento permaneceria a mesma?
O orçamento do cliente é de \(M=16000\). Para indicar quais dos fundos investir, tomaremos como métrica de análise única e exclusiva a projeção futura de ganhos do fundo. Sendo assim, vamos estabelecer a relação que descreve os ganhos ao tempo \(n\). O Fundo A tem regime de juros simples e não há cobrança de entrada. Logo, a expressão do seu valor futuro seria
\[ FVA_{n} = M+M\cdot n\cdot 0.12=M(1+n\cdot i). \]
No caso do Fundo B temos
\[ \begin{align} FVB_{n} & = (M-4000)\cdot(1+0.1)^n. \end{align} \]
Se \(FVA_{n}>FVB_{n}\) então nossa indicação será o Fundo A e se for o inverso \(FVA_{n}<FVB_{n}\) indicaremos o Fundo B. Pelo tempo de vigência do Fundo A temos \(n=17\) e taxa de juros \(i=0.12\) a.a. No caso do Fundo B temos \(n=15\) e uma taxa de juros de \(i=0.1\) a.a. Avaliando os respectivos fundos temos
\[ \begin{align} FVA_{n} & = 16000\cdot(1+17\cdot 0.12)\\ FVB_{n} & = 12000\cdot(1+0.1)^{15}. \end{align} \]
Podemos computar os valores futuros por meio da calculadora Hp12c. Primeiramente pressione os botões  para limpar os registros da memória. Para o Fundo A digite a seguinte sequência
para limpar os registros da memória. Para o Fundo A digite a seguinte sequência 17 ENTER 0.12 x 1 + 16000 x. O resultado final desta operação provê \(FVA_{n}=48640\). Já para o Fundo B, podemos utilizar as funções financeiras já definidas na calculadora. Nesse caso, é suficiente informar os valores do aporte inicial, a taxa de juros empregada e o total de períodos investido. Sendo assim, para informar esses respectivos valores digite 12000  e
e 10  e
e 15  e ao final para computar o valor futuro tecle
e ao final para computar o valor futuro tecle  . O resultado dessa operação é \(FVB_{n}=50127\). Todavia, note que o resultado exibido no display possui sinal negativo. Por quê?
. O resultado dessa operação é \(FVB_{n}=50127\). Todavia, note que o resultado exibido no display possui sinal negativo. Por quê?
Desta modo, verifica-se que \(FVA_{n}<FVB_{n}\). Sendo assim, sob essa ótica recomendamos o Fundo B para investir. Ele se mostra vantajoso mesmo apesar de apresentar uma taxa de juros menor e de cobrar uma tarifa para ingressar no fundo.
Exemplo 3.2 Um investidor realiza duas aplicações financeiras em renda fixa. A primeira é feita com um montante total de R$ 120.000,00 no ativo M. Este paga juros de 6% ao semestre e possui um período total de 5 anos. A segunda aplicação é feita no ativo W, com um aporte superior ao M, totalizando R$ 150.000,00. O ativo W remunera com juros de 11% ao semestre durante um período de apenas um ano e meio. Entretanto, esta aplicação só é iniciada depois de dois anos e meio. Ambos os ativos remuneram com juros via regime composto.
(A). Ao resgatar ambas as aplicações, M e W, qual deles apresenta o maior montante final?
Primeiramente, para sintetizar toda operação traçamos o diagrama de fluxo de caixa.
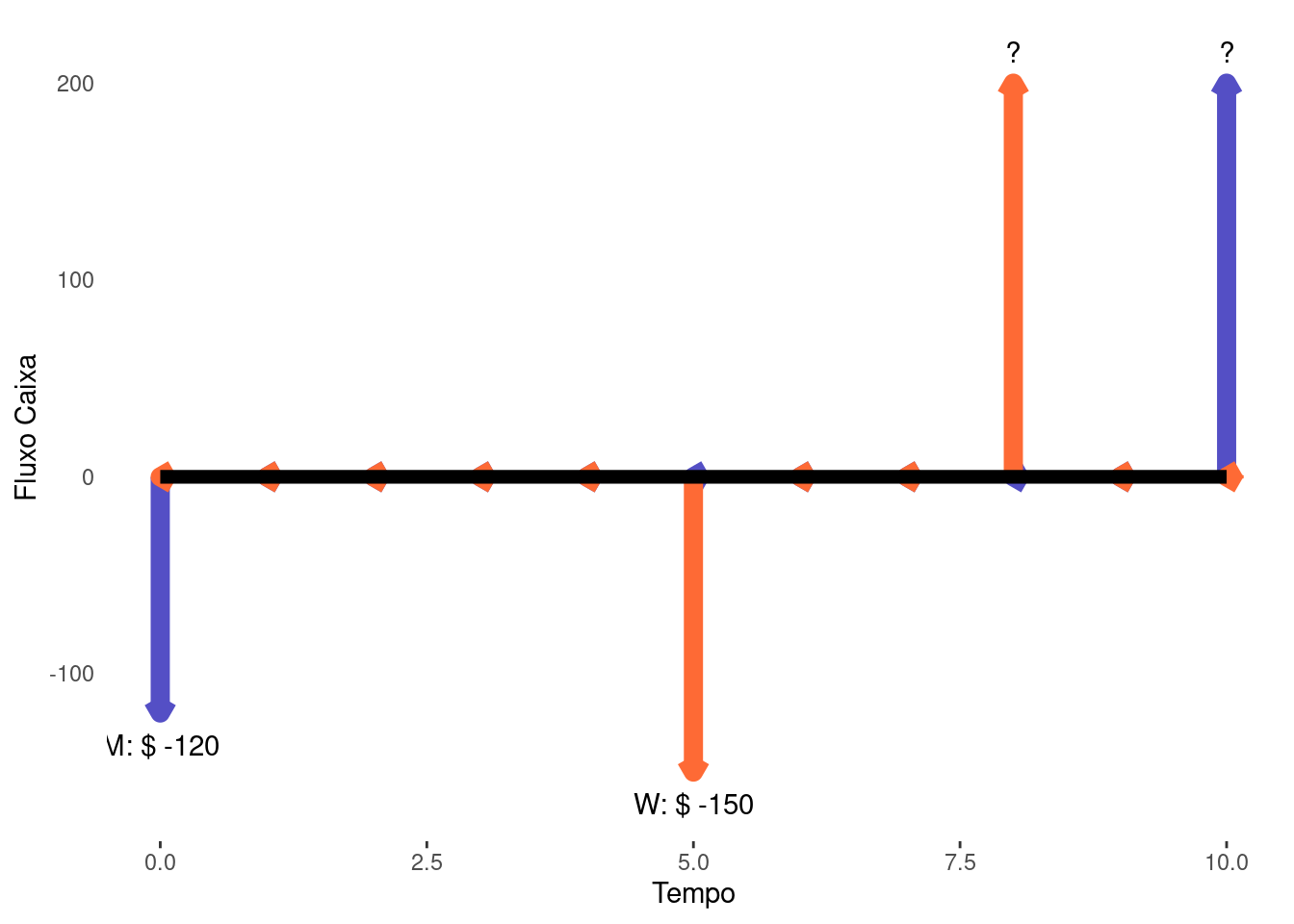
Para calcular os valores futuros de M e W devemos empregar a Equação 3.3. Contudo, para realizarmos comparações entre os ativos no tempo, necessitamos ajusta-los para um índice comum. Desta forma, escrevemos as equações de \(FV\) de cada ativo por
\[ \begin{align} FVM_{t} & = 120000\cdot(1+0.06)^t\\ FVW_{t} & = 150000\cdot(1+0.11)^{\delta_{t}}. \end{align} \tag{3.4}\]
O índice comum entre M e W é \(t\) e \(\delta_{t}=\min\left(\max\left(t-5,0\right),3\right)\) para \(t=1,2,...10\). O montante final de cada ativo transcorridos 5 anos é computado substituindo \(t=10\) na equação acima. Logo,
\[ \begin{align} FVM_{t=10} & = 120000\cdot(1+0.06)^{10}=214.901,70\\ FVW_{t=10} & = 150000\cdot(1+0.11)^{\delta_{10}}=205.144,70. \end{align} \] Note que para \(\delta_{10}=3\). Portanto, transcorridos 5 anos, o ativo M apresentará o maior montante final.
(B). Existe algum instante de tempo em que ambos os investimentos apresentavam o mesmo montante? Se sim em que momento e qual seria esse valor? Em caso negativo qual a menor diferença entre esses montantes ao longo do tempo?
Para descobrir o momento, caso exista, no qual tanto M e W possuam o mesmo montante é equivalente a encontrar o valor de \(t\) tal que \(FVM_{t}=FVW_{t}\). Pelo item anterior temos as expressões para lado da igualdade de modo que
\[ \begin{align} FVM_{t} = FVW_{t} & \Leftrightarrow 120000\cdot(1+0.06)^t = 150000\cdot(1+0.11)^{\delta_{t}}\\ \end{align} \tag{3.5}\]
Pelo item anterior e pelas informações fornecidas, caso exista um valor de \(t\) que satisfaça a equação acima, ele deve estar no intervalo \(t\in(5,10]\). Sabemos que para o ativo W seu montante máximo é obtido em \(t=8\) e além disso esse mesmo valor é igual em \(t=10\), então pelo item anterior \(FVW_{t=8}=205.144,70\). O montante do ativo M no instante \(t=8\) é facilmente calculado por meio da Equação 3.4. Logo, \(FVM_{t=8}=191.261,80\). Repare que entre \(t=8\) e \(t=10\) o montante do ativo M passa a ser maior que W pois tanto \(FVM_{t}\) quanto \(FVW_{t}\) são contínuas. Além disso, ambas funções são monotonicamente crescentes. Portanto, podemos afirmar que existe um valor de \(t\) que satisfaz a Equação 3.5 no intervalo \(t\in(8,10]\) e que ele é único. Desta forma, reescrevendo a Equação 3.5 para \(8<t\leq 10\) temos
\[ \begin{align} 120000\cdot(1+0.06)^t & = 205.144,70\\ (1.06)^t & = 1.71\\ t\cdot \log(1.06) = \log(1.71)\\ t=\frac{\log(1.71)}{\log(1.06)}\\ t=9.2. \end{align} \] Agora, para o intervalo \(t\in(5,8]\) realizamos o procedimento análogo. No instante de tempo \(t=5\) o montante do ativo M corresponde ao valor de \(FVW_{t=5}=160587\). No mesmo instante o ativo W encerra seu período de carência e inicia seu processo de remuneração, logo, seu valor é de \(FVW_{t=5}=150000\). Seguindo, para a outra extremidade do intervalo \(t\in(5,8]\) temos o instante \(t=8\) que já temos calculados (\(FVM_{t=8}=191.261,80\) e \(FVW_{t=8}=205.144,70\)). Novamente, temos a situação em que um dos ativos no primeiro instante encontra-se abaixo e ao final desse intervalo encontra-se acima, logo deve haver um instante de tempo \(t\) que há o cruzamento entre os montantes desses dois ativos. O W no primeiro momento possui um montante menor que M e ao final do intervalo \(t\in(5,8]\) tem um montante maior. Repare que neste intervalo a função que descreve a evolução do montante W é \(150000(1+0.11)^{t-5}\). Logo, calculamos o ponto do tempo \(t\) que ocorre o cruzamento da seguinte forma
\[ \begin{align} 120000\cdot(1+0.06)^t & = 150000(1+0.11)^{t-5}\\ (1.06)^t & = 1.25\cdot(1.11)^{t-5}\\ t\cdot \log(1.06) & = \log(1.25) + (t-5)\log(1.11)\\ t \left[\log(1.06)-\log(1.11)\right] & =\log(1.25)-5\cdot\log(1.11)\\ -t \cdot 0.0461 & =-0.2986\\ t &= 6.48. \end{align} \]
Portanto, durante quase toda a década de investimento (década = 10 anos) o ativo M apresentava um montante maior do que W. Até que no tempo \(t=6.48\) o montante do ativo W passa a ser maior que o do ativo M. Em outras palavras, esta mudança ocorre após 6 anos 5 meses e 25 dias. Essa situação se permanece até o instante de tempo \(t=9.2\) onde novamente o ativo M passa a possuir um montante de seus ativos superiores ao do W. Isto só ocorre somente 9 anos 2 meses e 14 dias depois que se iniciaram os investimentos. Na Figura 3.1 podemos observar a evolução de ambos os ativos M e W ao longo dos 10 anos e os momentos em que há os cruzamentos entre os respectivos montantes. Analise as curvas do gráfico e veja se o resultado de nossos cálculos estão coerentes.
3.2 Encontrando a Fórmula do Valor Futuro
Um questionamento importante que surge quando construímos a fórmula do valor futuro \(FV\) é como podemos garantir que a expressão da Equação 3.2 seja válida para todo \(n\in\mathbb{N}\). Uma possibilidade seria verificar a validade da relação para \(n=4\) e depois para \(n=5\) e seguir assim a de eterno. Contudo, esta é uma missão impossível visto que teríamos que checar infinitos valores. Para evitar tal incursão, podemos recorrer ao poderoso princípio de indução matemática para provar que relação estabelecida por essa equação será sempre válida.
A indução é uma ferramenta que nos permite provar formalmente diversas relações matemáticas. Basicamente, a indução busca verificar se uma dada proposição, construída por uma sucessão de valores de um conjunto discreto, permanece válida para todos os elementos desse conjunto. Assim, o método examina primeiramente para um determinado \(n\) como \(n=1\). Em seguida, assume-se por hipótese que a relação também é válida para algum \(n>1\). Caso verifique que essa relação se mantém verdadeira para o seu sucessor \(n+1\), então a relação será válida para toda coleção de \(n\).
De uma forma mais intuitiva, o princípio da indução funciona como o efeito dominó. Imagine que exista um conjunto de peças de dominó todas enfileiradas e enumeradas por \(n\) onde \(n=1,2,3,4,....\), ou seja, infinitas peças. Suponha que podemos verificar que a primeira peça \(n=1\) quando cai derruba a segunda. Calma! Ainda não podemos dizer que todas caem pois pode haver alguma peça que ao cair não empurre a sua sucessora. Então considere também que podemos selecionar uma peça qualquer, digamos \(n=n_{s}\). Vamos assumir por hipótese como sendo verdade o fato de que ao empurrar a peça \(n_{s}\) a gente consiga derrubar sua sucessora \(n_{s}+1\). Se mostrarmos que \(n_{s}+1\) também derruba sua sucessora utilizando a nossa hipótese, então ao voltar para a primeira peça \(n=1\) e constatar como verdadeira teremos certeza que ela derrubará sua sucessora também \(n=2\). Novamente aplicando a mesma ideia \(n=2\) derrubará \(n=3\). Desta forma, teremos uma cadeia de eventos nos quais cada peça segue derrubando a próxima criando assim o efeito dominó.
De maneira análoga, se considerarmos cada peça de dominó como sendo um período em que a Equação 3.2 avalia o montante, então teremos provado sua validade para todo \(n\in\mathbb{N}\). Essa será, portanto, nossa estratégia para realizar nossa demonstração.
Proposição 3.1 (Princípio da Indução Matemática) Axioma: Seja \(A\) um subconjunto de \(\mathbb{N}\). Se \(1\in A\) e se, além disso, \(A\) contém todos os sucessores dos seus elementos, então \(A=\mathbb{N}\).
Princípio da Indução Finita: Seja \(n_{0}\) um inteiro positivo. Suponhamos que, para \(n\geq n_{0}\) seja dada uma proposição \(P(n)\). Suponha ainda que se pode verificar as seguintes propriedades:
\(P(n_{0})\) é verdadeira
Se \(P(n)\) é verdadeira então \(P(n+1)\) também é verdadeira, para todo \(n>n_{0}\).
Então \(P(n)\) é verdadeira para qualquer \(n>n_{0}\).
Em nosso caso, do ponto de vista formal, precisamos saber se a relação dada na Equação 3.2 é válida para todos os valores \(n=1,2,3,...\) (\(n\in \mathbb{N}\)). Seguindo o princípio da indução, suponhamos que para algum \(n\) a relação dada na Equação 3.2 seja verdadeira. Assim, vamos verificar se a relação se mantém para \(n+1\).
\[ \begin{align} FV_{n}\cdot(1+i) & = V_{0}(1+i)^n(1+i)\\ & = V_{0}(1+i)^{n+1}=FV_{n+1}. \end{align} \]
Consequentemente, demonstramos por indução matemática que a Equação 3.2 é válida para todos os valores \(n=1,2,3,...\).
3.3 Exercícios
Exercício 3.1 A partir da Equação 3.3 que descreve o valor futuro \(FV\) de um ativo, podemos verificar que seu comportamento é em função dos períodos \(n\).
Exercício 3.2
Com base nos resultados apresentados no gráfico e nas tabelas exibidas na Seção 3.1, qual resposta é a mais adequada?Exercício 3.3 Um título de dívida de uma grande empresa, chamada \(\beta\), com valor de face de 10.000,00 e vencimento em 18 meses, está sendo negociada em janeiro no mercado com valores praticamente alinhados aos juros do título do tesouro. A taxa de juros do tesouro é de 1% ao mês. Considerando o risco do título de dívida da empresa \(\beta\) está equiparado ao do tesouro, responda as questões abaixo:
Qual o valor de cada título da dívida da empresa \(\beta\)?
Transcorridos 6 meses sem mudanças significativas na economia, qual o valor desse título de dívida da empresa \(\beta\)?
Restando 6 meses para o vencimento da dívida, o governo toma medidas para aquecer a economia reduzindo os juros para para 0.15% ao mês. Supondo que um investidor tenha em sua carteira 4 títulos de dívida da empresa \(\beta\) comprada em janeiro, contrate seus serviços de consultoria financeira. Diante desse novo cenário apresentado qual será sua análise e sugestão para esse cliente.
- O valor de mercado do título \(T_{n}\) é computado trazendo a cifra de resgate de 10.000 a valor presente. Considerando desconto composto racional, período de 18 meses e a equiparação de taxa de juros de 1% ao mês temos
\[ \begin{align} T_{n} & = \frac{T_{0}}{(1+i)^{n}}= \frac{10.000}{(1+0.01)^{18}} = 8360.17. \end{align} \]
No caso de desconto racional simples a lógica de operação permanece.
\[ \begin{align} \widetilde{T}_{n} & = \frac{T_{0}}{(1+n\cdot i)}= \frac{10.000}{(1+18\cdot 0.01)} = 8474.58. \end{align} \]
- Mantendo o título por mais 6 meses, a única coisa que se altera com relação ao item anterior é o valor de \(n\).
\[ \begin{align} T_{n} & = \frac{T_{0}}{(1+i)^{n}}= \frac{10.000}{(1+0.01)^{12}} = 8360.17. \end{align} \]
No caso de desconto racional simples.
\[ \begin{align} \widetilde{T}_{n} & = \frac{T_{0}}{(1+n\cdot i)}= \frac{10.000}{(1+12\cdot 0.01)} = 8928.57. \end{align} \]
- Com a queda da taxa de juros há um deslocamento do equilíbrio dos preços. Visto que o título de dívida da empresa \(\beta\) permanece remunerando a 1%, os agentes recebem um incentivo para trocar títulos do tesouro pelo título da empresa \(\beta\). Como consequência natural, um aumento da demanda por este papel é esperada, o que pressiona para cima os preços desses papéis. No entanto, esse aumento tem um limite bem definido e é alcançado quando estabelece o equilíbrio com outro título com mesmo patamar de risco. Em nosso caso, o título de referência é do tesouro, logo o novo preço de equilíbrio do título \(T'_{n}\) é computado da seguinte forma
\[ \begin{align} T'_{n} & = \frac{T_{0}}{(1+i')^{n}}= \frac{10.000}{(1+0.0015)^{6}} = 9940.21. \end{align} \]
No caso de desconto racional simples.
\[ \begin{align} T'_{n} & = \frac{T_{0}}{(1+i')^{n}}= \frac{10.000}{(1+6\cdot0.0015)} = 9940.36. \end{align} \]
Repare que há uma relação inversa entre a taxa de juros e o valor do título de dívida da empresa. Considerando que o valor do título foi adquirido por 8360.17, uma venda desse ativo no mercado por 9940.21 conferiria um retorno de 18.9% em 12 meses. Na expectativa de um horizonte de tempo de 18 meses, haveria ainda uma possibilidade de auferir ganhos adcionais. Isso poderia ser feito investindo mais 6 meses com taxa de mercado 0.015%. Dessa forma, uma possibilidade seria aconselhar pela venda do ativo. Alternativamente, manter o ativo até o vencimento (Yield to Maturity) seria ligeiramente menor.
Exercício 3.4 Um grupo de estudantes de uma faculdade pensa em cobrar um valor único em uma data bem anterior ao dia da formatura. Este curso tem uma duração total de 9 semestres. A ideia é aproveitar uma oportunidade de investimento de 0.9% a.m. e comprar uma cota da aplicação por R$ 2000,00. Com a entrada de novos ingressantes, quando esse grupo deve realizar essa cobrança?
Temos os seguintes dados \(FV=2950\), \(PV=2000\) e uma taxa de juros \(i=0.009\).
\[ \begin{align} FV&=PV\cdot(1+i)^{t} \Leftrightarrow \frac{FV}{PV} = (1+i)^{t}\\ &\Leftrightarrow \log\left(\frac{FV}{PV}\right) = \log(1+i)^{t}\\ &\Leftrightarrow \log\left(FV\right)-\log\left(PV\right) = t\log\left(1+i\right)\\ &\Leftrightarrow t = \frac{\log\left(FV\right)-\log\left(PV\right)}{\log\left(1+i\right)}= \frac{\log\left(2950\right)-\log\left(2000\right)}{\log\left(1.009\right)}\\ &\Leftrightarrow t = 43.37 \\ &\Rightarrow \lceil t \rceil =\lceil 43.37 \rceil =44. \end{align} \] Como o curso tem 54 meses, então com 10=54-44 meses após os calouros ingressarem seria o limite para realizar a cobrança.
Exercício 3.5 Dona Vera sempre sonhou em ser trader. Ao iniciar sua carreira, ela abriu uma conta numa corretora para operar no mercado. Em sua primeira aplicação, ela gerou um montante de 16000 durante exato 1 ano. Já na segunda aplicação, Dona Vera aumentou o aporte de investimento inicial em 20% quando comparada a primeira. O resultado foi um montante de 19000 depois de 8 meses, com a mesma taxa da primeira aplicação. Encontre a taxa de juros que Dona Vera obteve em seus investimentos (Lembre-se que sempre será juros compostos. Juros simples somente quando for expressamente colocado.).
Escreva as equações para cada uma das operações. Cada equação terá duas variáveis, \(P_{0}\) e \(i\) e juntas compõe um sistema de equações. Para resolver esse sistema, em uma das equações (digamos a primeira equação) isole uma variável em termos da outra (digamos \(P_{0}\) em termos de \(i\)) e substitua na outra equação (digamos a segunda equação). Pronto, a segunda equação ficará somente em função de uma única variável (digamos \(i\)). Agora é possível resolver, basta isolar a variável de interesse nesta equação (digamos \(i\)) e descobrir o seu valor. Com este valor em mãos, volte para a equação original (digamos a primeira) substitua pela variável correspondente (digamos \(i\)). Agora é possível resolver, basta isolar a variável que falta descobrir seu valor (digamos \(P_{0}\)). Pronto, teremos tanto os valores de \(P_{0}\) quanto de \(i\).
Exercício 3.6 Carlinha, a bisneta de dona Vera, ao final de um ano necessita pagar pelas chaves de um Studio que adquiriu no valor de 140000. Preocupada, Carlinha pede ajuda ao seu coach. Se você fosse o coach como procederia nas seguintes hipóteses:
Quanto você indicaria para Carlinha aplicar hoje em um fundo de investimento que paga 1.8% a.m. e que não opera cripto moeda para poder quitar seu débito?
Se no final do 7 mês Carlinha garantir levantar 80 mil reais por meio de uma vaquinha junto aos seus seguidores. Confiando nesse dinheiro para poder adicionar no fundo de investimento, qual o valor que deve ser investido hoje?
Monte o diagrama de fluxo de caixa.
