1 Introdução
Na natureza nos deparamos com diversas situações que envolvem incertezas. Elas ocorrem tanto em processos físicos como a termodinâmica quanto nos fenômenos sociais como a economia. Em um sentido mais amplo, denominamos essas situações como experimentos ou fenômenos aleatórios. Temos, portanto dois elementos presentes em experimentos aleatórios a ocorrência de um determinado evento e ligado a ele uma certa noção de incerteza. Para lidar com problemas envolvendo fenômenos aleatórios lançamos mão da probabilidade. Posto isso, uma pergunta pode vir a surgir. Por que se utilizar de ferramentas e artifícios para tratar de algo que não temos controle ou gerência?
Antes de prosseguímos, é importante que o aluno comece incorporar em seu olhar diante dos problemas o carácter incerto aos quais nos são impostos em que parte de são devidas a nossas ações mas outra parte está sujeita de fato um conjunto enormes de fatores que de fato guiam parte das nossas vidas. Ainda que se atribua o elemento da incerteza a alguma vertente religiosa nossos controles sobre eles não nulos. Com essa melhor compreensão podemos ter uma melhor capacidade de entender os resultados nos mais amplos setores da vida.
Os problemas do mundo que nos deparamos quase indubitavelmente envolve incertezas e de maneira indissociável de suma complexidade. O processo para tratar tais problemas, inicia-se com uma reformulação abstrata e simplificada da realidade de maneira a nos concentrar nos principais fatores que regem ou impactam sobre o fenômeno aleatório estudado.
A estas abstrações da realidade damos o nome de modelo. Em outras palavras, um modelo é toda e qualquer tentativa de descrever a realidade, mas jamais uma busca de recriá-la de maneira fidedigna. Diante deste cenário, um famoso estatístico britânico chamado de George E. P. Box resumiu com toda primazia ao proferir as seguintes palavras “All models are wrong, but some are useful”. A essência de todo e qualquer modelagem ou método estatístico aplicado reside nessa frase. Pois um modelo é apenas uma tentativa de descrever um objeto de modo simplificado no qual é impossível defini-lo em sua completude de detalhes. Todavia, ainda que fosse possível, teríamos o próprio objeto em si e concomitantemente não teríamos mais o modelo. Ao criarmos um modelo para lidar com algum objeto ou fenômeno estamos realizando um processo de abstração da realidade.

1.1 Modelo Matemático de um Experimento
O experimento que consiste em observar o resultado de um determinado processo que ocorre sob certas condições fixas e sobre as quais não temos qualquer ingerência denominamos por fenômeno ou experimento aleatória. Apesar de não ser factível a determinação do resultado de um experimento aleatório é possível postular todos os seus resultados elementares e indivisível descrito mediante um determinado modelo. O conjunto formado por todos os resultados possíveis de um experimento aleatório é denominado espaço amostral e é denotado por \(\Omega\).
Cada possível resultado do experimento chamamos por ponto ou elemento do espaço amostral e denotamos \(w\in\Omega\) para designar que o elemento \(w\) pertence ao conjunto \(\Omega\). Eles devem corresponder a um e somente um elemento de \(\Omega\). Além disso, resultados distintos equivalem a pontos \(w\) distintos em \(\Omega\), ou seja, não pode representar mais de resultado.
Através dos elementos que compõe o espaço amostral de um fenômeno aleatório, podemos caracterizá-lo como um conjunto
Enumerável: Finito ou Infinito
Não Enumerável
Um conjunto é dito enumerável infinito quando podemos estabelecer uma bijeção entre os elementos do conjunto \(\Omega\) e os números naturais \(\mathbb{N}\) tais que \(f:\mathbb{N}\rightarrow \Omega\). Caso possamos estabelecer uma relação biunívoca de um subconjunto finito dos naturais onde \(g: A\subset\mathbb{N}\rightarrow\Omega\), então dizemos que \(\Omega\) é um conjunto enumerável finito.
Exemplo 1.1
Enumerável finito: Em um experimento de observar lançamento de um dado \(\Omega=\{1,2,3,4,5,6\}\)
Enumerável infinito: Número de \(n\) cometas observados dentro de um ano \(\Omega=\{n,\text{ onde }n\in\mathbb{N}\}\)
Não Enumerável: Tempo \(t\) até o surgimento do próximo terremoto \(\Omega=\{t,\text{ onde }t\in\mathbb{R}^{+}\}\)
O conjunto composto por nenhum elemento é chamado de conjunto vazio e é denotado por \(\emptyset\). Um conjunto \(A\) de elementos que está contido inteiramente em \(\Omega\) é denominado como um subconjunto do espaço amostral e é escrito por \(A\subset\Omega\).
Definição 1.1 Seja \(\Omega\) o espaço amostral de um experimento aleatório. Todo subconjunto \(A\subset \Omega\) é chamado de evento aleatório.
O evento \(\Omega\) é o evento certo de um experimento e \(\emptyset\) o evento impossível.
Exemplo 1.2 Em um experimento, considere o espaço amostral definido pelo conjunto \(\Omega=\{2,4,6,8,11\}\). Verifique as afirmativas a seguir.
\(3\in\Omega\,\,\)
\(8\notin\Omega\,\,\)
\(6\notin\Omega\,\,\)
\(\{6,1,11\}\subset\Omega\,\,\)
\(\{2,11,6,4\}\not\subset\Omega\,\,\)
Em diversos momentos será necessário realizar operações algébricas envolvendo conjuntos. Dentre as mais importantes temos
- \(\bar{A}\) ou \(A^{c}\) é chamado de conjunto complementar. Seus elementos são definidos por todos aqueles que concomitantemente pertence ao espaço amostral e não pertence ao conjunto \(A\)
- \(A_{1}\cup A_{2}\cup ,...,A_{n}\) ou \(\displaystyle\bigcup_{i=1}^{n}\) é a união dos conjuntos \(A_{i}\) onde \(i=1,...,n\) representa todos os pontos de \(\Omega\) e que também pertencem a pelo menos um dos \(A_{i}\) .
- \(A_{1}\cap A_{2}\cap ,...,\cap A_{n}\) ou \(\displaystyle\bigcap_{i=1}^{n}\) é denominada intersecção do conjuntos \(A_{i}\) onde \(i=1,...,n\) e representa todos os pontos de \(\Omega\) e simultaneamente todos os \(A_{i}\) .
- \(A-B\) ou \(A\cap B^{c}=AB^{c}\) é a diferença entre \(A\) e \(B\) isto é todos pontos de pertence a \(A\) e simultaneamente não pertence a \(A\)
- \(A\bigtriangleup B\) ou \(A\cap B^{c}\cup A^{c}\cap B\) é a diferença simétrica entre \(A\) e \(B\), isto é, todos pontos \(\Omega\) e que pertence somente \(A\) ou somente a \(B\) mas não a ambos simultaneamente. Pode ser interpretado como o ou exclusivo (XOR).
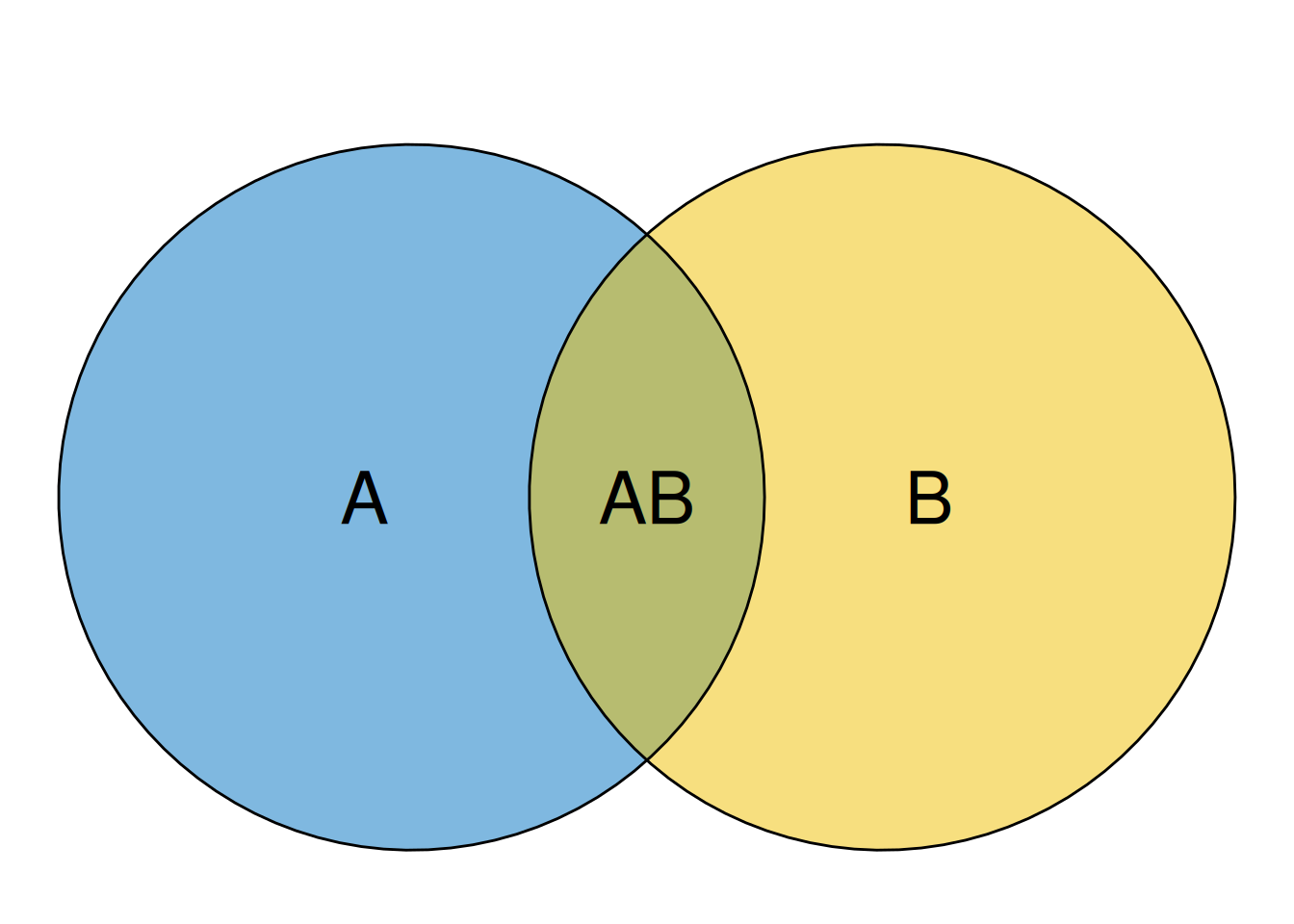
Uma maneira gráfica de exibir as operações envolvendo conjuntos é por meio do diagrama de Venn. Neste diagrama, os elementos pertencentes ao um conjunto são representados através das áreas das formas geométricas com usas linhas fechadas (conjunto compacto). Quando nos referimos a probabilidade, usualmente representamos o espaço amostral \(\Omega\) com um retângulo maior. Consequentemente, todas as outras representações estão contidas nesse retângulo. A figura ao lado ilustra o diagrama para representar dos conjuntos \(A\cap B\), \(A\) e \(B\) por meio do diagrama de Venn. \[ A \text{ e }B \text{ disjuntos } \Leftrightarrow A\cap B=\emptyset. \] Dois conjuntos são ditos disjuntos ou mutualmente excludente se sua intersecção é o conjunto vazio \(\emptyset\), como mostrado na equação acima.
Dizemos que \(A_{1}\), \(A_{2}\),…, \(A_{n}\) é uma partição de \(\Omega\) se são disjuntos e se a sua união formão o conjunto \(\Omega\).
\[ \displaystyle\bigcup_{i=1}^{n} A_{i} = \Omega \text{ onde } A_{i}\cap A_{j}=\emptyset\,\,\, \forall\, i\neq j. \]
A figura abaixo mostra um exemplo de uma partição do espaço amostral.
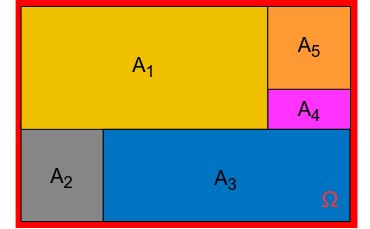
Note que os conjuntos \(A_1, A_2, A_3, A_4\) e \(A_5\) não possuem intersecção entre si, isto é, \(A_{k}\cap A_{j}=\emptyset\) quando \(k\neq j\). Além disso,
\[ \displaystyle\bigcup_{i=1}^{5} A_{i} = \Omega. \]
Em diversos casos necessitamos computar o conjunto complementar resultante de uma operação envolvendo união ou intersecção. Neste sentido, as leis de Morgan descrevem as seguintes relações
\[ \left(\displaystyle\bigcup_{i=1}^{n} A_{i}\right)^{c} = \left(\displaystyle\bigcap_{i=1}^{n} A^{c}_{i}\right) \]
\[ \left(\displaystyle\bigcap_{i=1}^{n} A_{i}\right)^{c} = \left(\displaystyle\bigcup_{i=1}^{n} A^{c}_{i}\right) \]
Vamos a seguir apresentar uma classe de subconjuntos do espaço amostral com algumas propriedades interessante. Ela será essencial para a definição axiomática de Kolmogorov.
Definição 1.2 Uma classe de subconjuntos de \(\Omega\) representado por \(\mathcal{F}\) é denominado um \(\sigma\)-álgebra se satisfaz as seguintes propriedades :
\(\Omega\in \mathcal{F}\)
Se \(A\in\mathcal{F} \Rightarrow A^{c}\in\mathcal{F}\)
Se \(A_{i}\in\mathcal{F}, i\geq 1 \Rightarrow \displaystyle\bigcup_{i=1}^{\infty}A_{i}\in\mathcal{F}\)
Uma função muito útil é a chamada função indicadora
\[ \begin{equation*} I_{A}(w) = \begin{cases} 1 \text{ se $w \in \Omega$,} \\ 0 \text{ se $w \notin \Omega$}. \end{cases} \end{equation*} \]
Em diversos momentos a utilização de funções indicadoras facilitam nossa interpretação ou facilita os cálculos.
Definição 1.3 Sejam \(A_{1}\), \(A_{2}\),…,\(A_{n}\) subconjuntos de \(\Omega\), isto é, eventos. Sendo \(A=\cup_{i=1}^{n}A_{i}\) e \(B=\cap_{i=1}^{n}A_{i}\) então
\(I_{A}(w)=1-\displaystyle{\prod}_{i=1}^{n}I_{A_{i}^{c}}(w)\)
\(I_{B}(w)=\displaystyle{\prod}_{i=1}^{n}I_{A_{i}^{c}}(w)\)
Usualmente estamos interessados em computar a probabilidade de um certo evento que envolve nosso cotidiano. Mesmo antes de abordar um conceito mais preciso de probabilidade (próximo capítulo), podemos estabelecer, de maneira intuitiva, que probabilidade pode ser computada através da razão entre a quantidade de casos favoráveis e o total de casos possíveis.
Nessa linha, suponha que em determinado experimento o espaço amostral seja \(\{w_{1},w_{2},...,w_{12}\}\). Considere também que o evento de interesse é representado por \(B=\{x_2, x_4, x_{6}\}\subset\Omega\). Assim, a probabilidade de ocorrência do evento \(B\) é denominado por \(P(B)\) pode ser calculado da seguinte forma: \[ P(B)=\frac{\text{Número de casos favoráveis}}{\text{Número total de casos}}=\frac{\sum_{i=1}^{n}I_B(w_{i})}{n}=\frac{3}{12}=25\%. \tag{1.1}\] Sendo assim, considere os seguinte exemplo.
Exemplo 1.3
Um carro de luxo sempre foi o sonho de Dick. Sem recursos para adquiri-lo, ele teve uma ideia, mas ficou inseguro quanto a suas chances. Para descobrir, Dick recorre a universitários e pergunta, qual a probabilidade de ganhar um carro de luxo diante da seguinte situação? Ao chegarmos em uma concessionária, buscamos o gerente e lhe fazemos a seguinte pergunta: “O senhor poderia, por gentileza ter a amabilidade de me franquear esse lindo carro de graça?”. Ao gerente compete essencialmente duas respostas, “Sim, claro, Padawan!” ou um sonoro “NÃO!”.

Portanto, teríamos o espaço amostral \(\Omega=\{\text{Sim; claro, Padawan!};\text{NÃO!}\}\). Sendo o subconjunto \(\{ \text{Sim, claro, Padawan!}\}\subset\Omega\) o nosso evento de interesse, então poderíamos ficar esperançosos visto que \[ \begin{split} P(\{\text{Sim, claro, Padawan!}\})&=\frac{ \# \{ \text{Sim, claro, Padawan! } \} }{ \# \{ \text{Sim, claro, Padawan!}; \text{ NÃO!} \}}\\ &=\frac{1}{2}=50\%. \end{split} \]
Apesar de animador, o resultado soa factível para você? Se há algum erro em nossa avaliação, qual seria essa falha? Por quê o mesmo raciocínio envolvendo uma moeda não nos estranharíamos?
Note que pela equação acima, fica evidente que estamos diante de espaço amostral \(\Omega\) enumerável finito. De outra forma, se fosse o caso de enumerado infinito não haveria como definir um valor para usar no denominador. A mesma situação ocorre quando temos um espaço amostral não enumerável. Pois neste caso não teríamos como contar quantos casos de um certo evento e ainda dividi-lo pela quantidade de elementos do espaço amostral no denominador.
No Exemplo 1.3 o resultado soa completamente estranho porque consideramos, inadvertidamente, todos os elementos do espaço amostral equiprováveis quando claramente não são. Todavia, quando estamos diante de um experimento aleatório com espaço amostral enumerado finito e equiprovável, então a probabilidade de qualquer evento é computada como na Equação 1.1. Em síntese, nestes casos podemos transcrever um problema de contagem, isto é, de análise combinatória.
Nos casos análogos envolvendo espaços amostrais enumerado infinito, a abordagem para calcular probabilidade envolveriaa noção de limites para calcular probabilidades. Já no caso de espaços amostrais não enumeráveis e equiprováveis a abordagem irá envolver a relação de comprimentos ou áreas, com relação a um valor total e de mesma dimensão.
