Modelagem Estatística

Introdução: conceitos e noções via raciocínio lógico e intuitivo

Prof. Yuri Maluf

Análise de Layout de Atendimento

No município de Cambará, a câmara municipal aprovou uma lei em 2018 que regulamenta sobre o tempo de espera para atendimento nas instituições bancários.

Lei Municipal de Cambará PR

Análise de Layout de Atendimento

A agência do banco ACME de Cambará PR vem enfrentando recorrentes notificações da prefeitura em virtude do tempo de espera excessivo no atendimento ao público. A agência Cambará dispõe de 2 funcionários para atendimento, o que é compatível a de outras cidades de porte similar. Insatisfeita com os índices, a sede do banco ACME exigiu melhorias para níveis satisfatórios num prazo de 2 meses. O diretor responsável da agência, por sua vez, convoca os gerentes para deliberarem sobre estratégias para mitigar o tempo de espera no atendimento. Após a reunião decidiu-se contratar uma consultoria para:

1. redesenhar os processos e métodos

2. montar um programa de treinamento

Apesar dos resultados positivos alcançados dentro de um mês, as reclamações pelo tempo de espera ainda continuavam frequentes e acima do estabelecido por lei como razoável. No relatória da consultoria, fica claro que a agência somente irá cumprir as exigências da sede se definir um layout eficiente. O relatório também sustenta que um atendente especializado demanda: 10 min no serviço A e 20min no serviço B. Ao passo que um funcionário generalista demanda: 11 min no serviço A e 28 min para o serviço B.

Análise de Layout de Atendimento

Restando apenas um mês, o diretor convoca os gerentes para definir o layout. Após muito debate propostas, um empasse se instalou entre os executivos para decidir entre layout definir.

Fila em série e atendimento generalista

Fila em paralelo e atendimento especializado

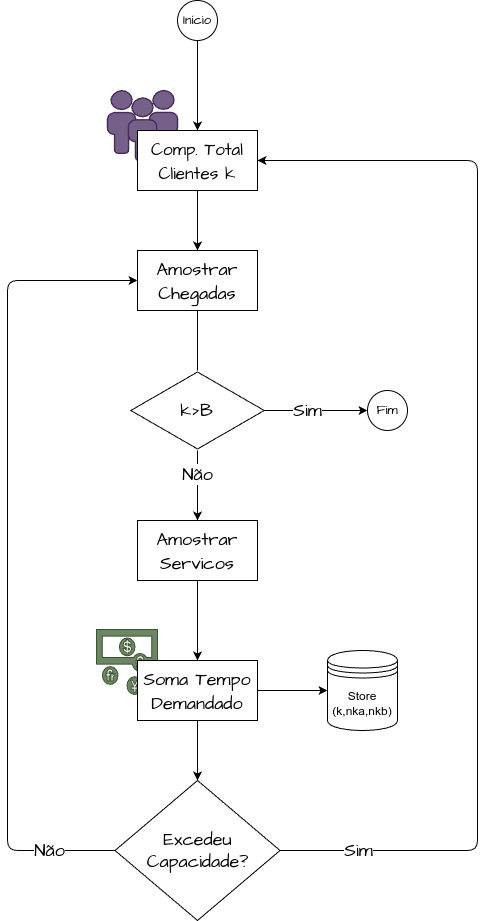
Simulação Fila Série - Algorítimo

Estimando o valor de \(\pi\)

Área do quadrado \(S\): \(A_{S}=2r\times 2r=4r^2\)

Área do círculo \(C\): \(A_{C}=\pi r^2 \Rightarrow \pi = \frac{A_{C}}{r^2}\)

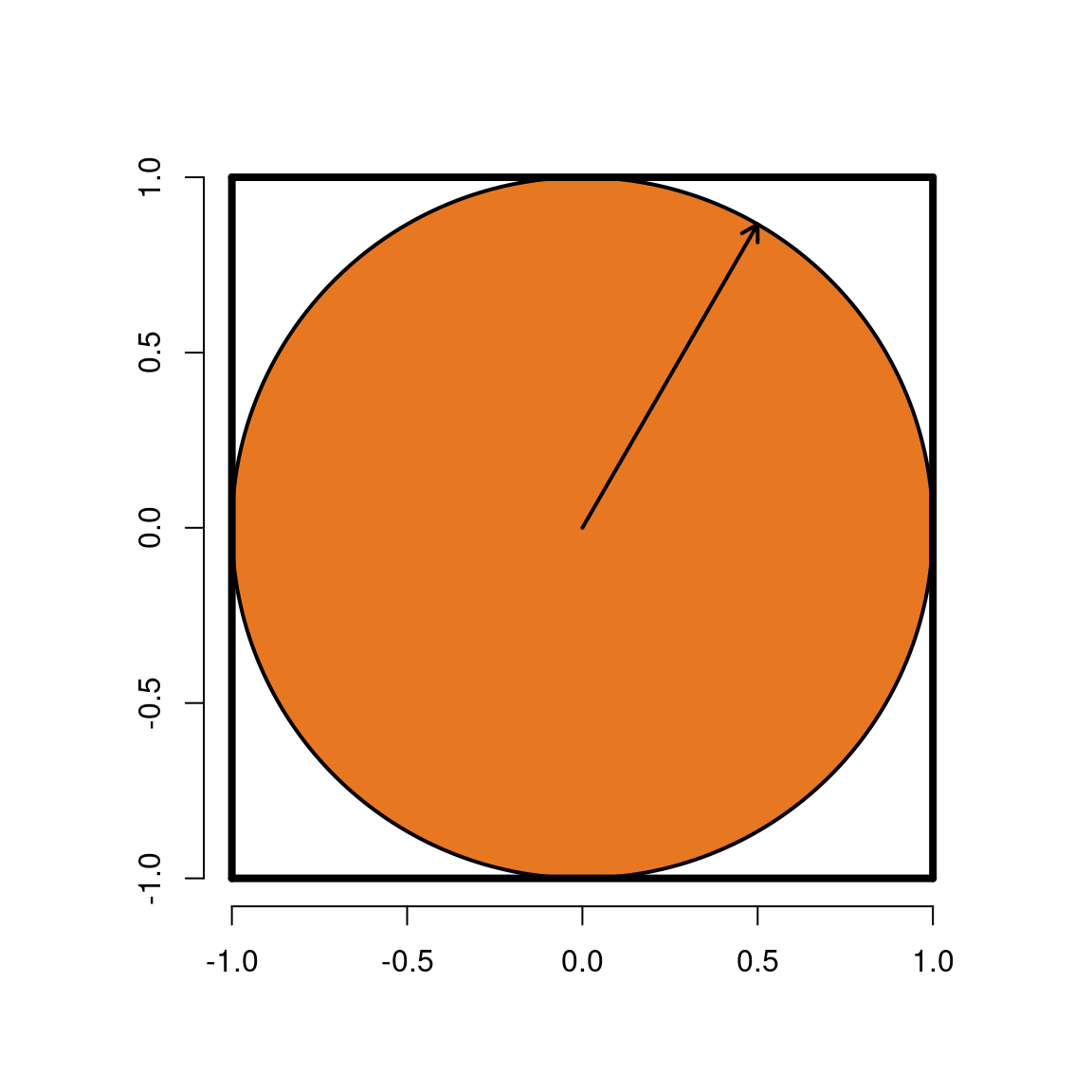
Substituindo \(r^2=A_{S}/4\) \[ \pi = 4\cdot\frac{A_{C}}{A_{S}}\leq 4. \] Como \(C\) está circunscrito a \(S\) então \(A_{C} \leq A_{S}\). Se um ponto dentro de \(S\) for selecionado aleatoriamente, a chances de estar dentro também de \(C\) é proporcional a \(A_{C}\). Um estimador com \(n\) pontos

\[ \hat{\pi}_{n} = 4\cdot\frac{ \#\left\{ a_i \in C \right\}}{n} \text{ onde } i=1,...,n. \]

Logo, o problema de estimar o valor de \(\pi\) pode ser trocado pelo problema de encontrar a área do círculo \(C\).

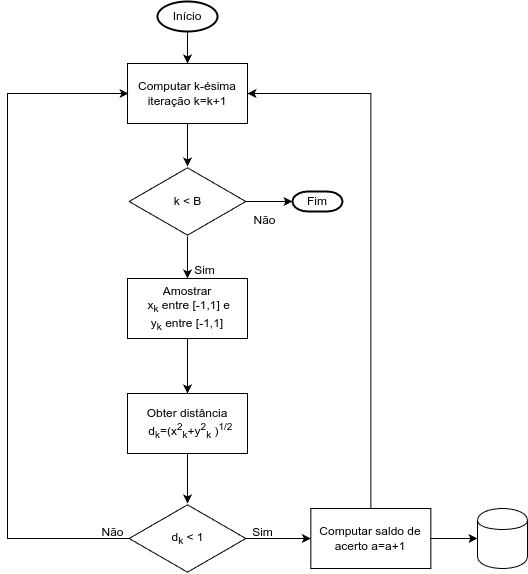
Estimando o valor de \(\pi\)

Fluxograma do estiimador de pi via simulação

Estimando o valor de \(\pi\)

Porta dos Desesperados

No quadro intitulado Porta dos Desesperados, o apresentador Sérgio Malandro trazia uma criança ao palco. Na brincadeira, a criança teria que adivinhar em qual das três portas estava o prêmio. Antes de abrir a porta, invariavelmente, Sérgio Malandro revelava uma das portas restantes, na qual seguramente estava vazia. Na sequência, o apresentador perguntava à criança se desejaria mudar de porta ou se manteria. Definida a resposta, então era aberta a porta dos desesperados.

As crianças que mantinham suas convicções em suas escolhas eram menos ou mais assertivas do que aquelas que mudavam de opinião, ou a adoção de qualquer estratégia conduz as mesmas probabilidades de ganho? Podemos utilizar de uma simulação para verificar se há alguma diferença significativamente entre elas.

Porta dos Desesperados

Fluxograma simulação das estratégias da porta dos desesperados.

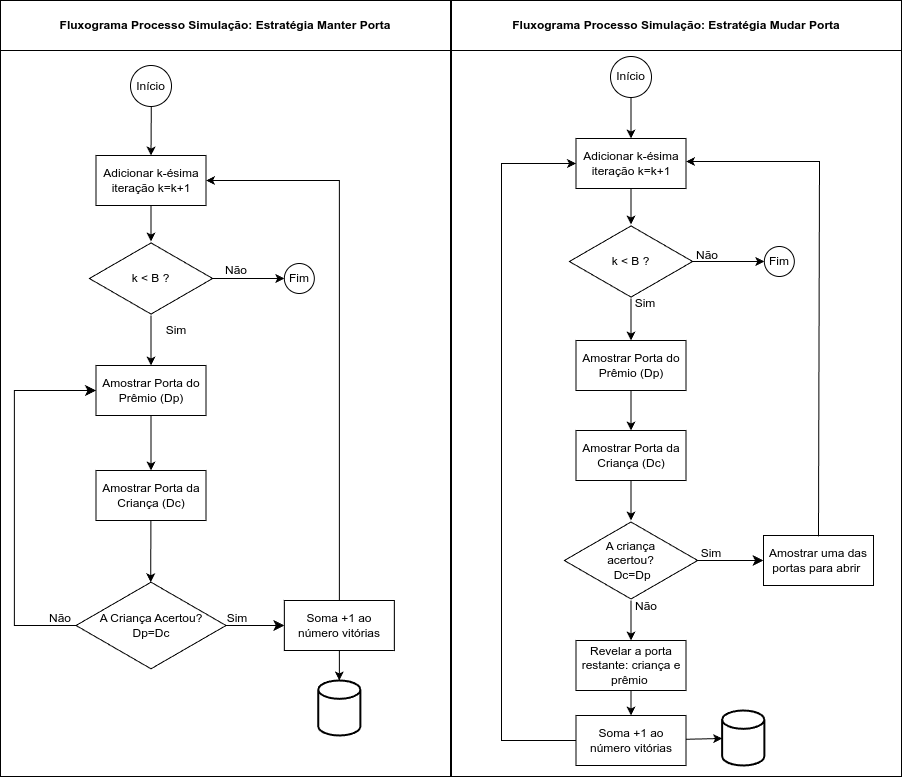
Porta dos Desesperados - Estratégia Manter

Para verificar o resultado de nossa simulação aperte o botão Run Code

Porta dos Desesperados - Estratégia Mudar

Lei Municipal de Cambará PR Fila em série e atendimento generalista Fila em paralelo e atendimento especializado Fluxograma do estiimador de pi via simulação Fluxograma simulação das estratégias da porta dos desesperados.