Introdução à Matemática Financeira

Conceitos Fundamentais

Prof. Yuri S. Maluf

Introdução

O campo da matemática financeira, em essência, trata-se da análise do valor do dinheiro ao longo do tempo. As ferramentas desenvolvidas pela matemática financeira permitem realizar análises e comparações dos diversos fluxos de entrada e saída de recursos no caixa em diversos momentos no tempo.

Fluxo de Caixa

Denomina-se fluxo de caixa (FC) o conjunto de entradas e saídas de recursos, com liquidez imediata, ao longo do tempo. A apreciação do fluxo de caixa pode envolver tanto movimento financeiro de uma empresa quanto de um fundo de investimentos, na gestão de projetos, operações financeiras, comerciais ou mesmo pessoais.

A elaboração e análise do F.C. é indispensável em diversas atividades empresariais sobre tudo no estudo de viabilidade econômico-financeira de projetos de investimentos.

A representação do fluxo de caixa é feita por tabelas, relatórios, quadros ou esquematicamente. O relatório contábil do fluxo de caixa é chamado de demonstração de fluxo de caixa (DFC). A representação esquemática do F.C. mais usual é feita por meio do diagrama de F.C..

Demonstração Contábeis

Demonstração do balanço patrimonial - BP
Demonstração do resultado do exercício - DRE
Demonstração do fluxo de caixa - DFC

Conceitos importantes
- Ativo: São os bens, direitos e valores que a empresa possui e podem ser convertidos em benefícios econômicos futuros.
- Passivo: São as obrigações e dívidas da empresa, ou seja, as contas a pagar e outras responsabilidades financeiras.

Estrutura do Balanço Patrimonial

Balanço Patrimonial - BP

Demonstração do Balanço Patrimonial

Balanço Patrimonial - BP

Estrutura do Resultado do Exercício

Estrutura DRE

Demonstração do Resultado do Exercício

Demonstração do Resultado do Exercício - DRE

Demonstração do Resultado do Exercício

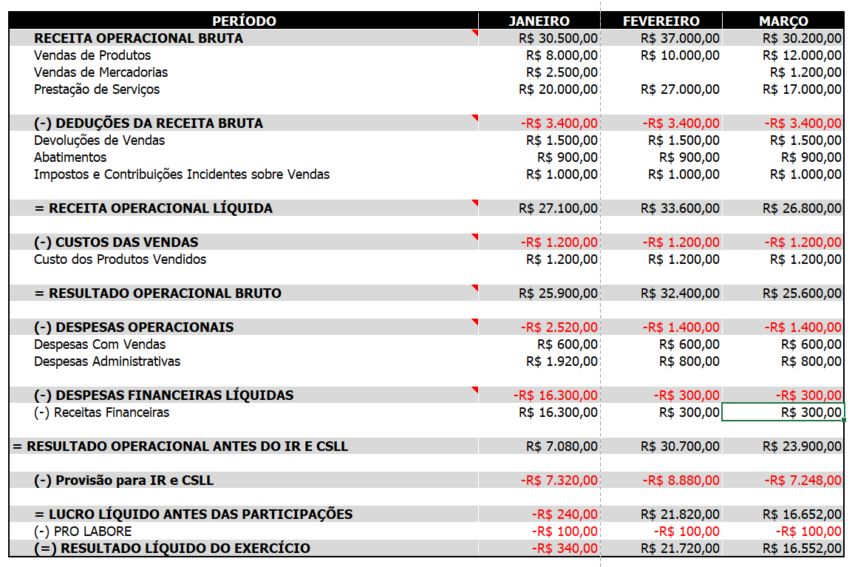
Demonstração do Resultado do Exercício - DRE

Demonstração do Fluxo de Caixa

Demonstração do Fluxo de Caixa DFC

Ideia de Fluxo

Fluxo de Campo

Diagrama de F.C.

O diagrama de fluxo de caixa adota a seguinte convenção:

A reta horizontal representa o tempo, dividido em períodos regulares e discretos.
Os intervalos de tempo são todos iguais.
Os valores monetários são referentes ao final do período. Isto é, a capitalização é realizada de forma descontínua.
As saídas de caixa são representadas com sinais negativos ( - ) e são indicadas com setas para baixo.
As entradas de caixa são representas com sinais positivos (+) e são indicadas com setas para cima.

Diagrama de F.C.

Dependendo do caso, empregamos as setas como:
- Saldo do fluxo de caixa. Desta forma, fica configurada no máximo uma seta por período.
- Os diversos fluxos ocorridos. Neste caso, teremos diversas setas por período.
O conjunto das setas, representando os saldos do fluxo, é geralmente chamado de série de pagamentos.

Diagrama de F.C.

Exemplo

Rubinho comprou seu carro em 10 parcelas de R$ 1.350,00 e uma entrada de R$ 5.010,00. Na 6ª parcela, ele vende seu carro para seu amigo Michael por R$ 18.310,00. Monte o diagrama de fluxo de caixa do Rubinho nesta operação.

Exemplo Resolução

Exercício

Uma empresa tem um projeto de investir na compra de uma máquina de produzir camisas. O valor da máquina somado aos gastos de instalação é de R$ 250 mil. Ela pode ser adquirida com uma entrada de R$ 50 mil e o restante em 2x de R$ 100 mil. Após sua compra é possível entrar em operação em 1 mês para começar as vendas das camisas.

Sabe-se que a máquina gera um fluxo de caixa positivo de R$ 20 mil por mês referente a sua produção. Com base nestas informações monte o diagrama de fluxo de caixa para este projeto de investimento.

Exercício Resolução

Exercício

O setor financeiro de uma empresa de evento analisa a viabilidade de um determinado show. Neste evento a empresa responsável pela montagem dos equipamentos e contratação de pessoal cobra 5x de R$ 100 mil sendo a 1ª parcela dois mês antes do evento. A equipe dos artistas recebem 50% com 1 mês antecedência e o restante no dia do evento, totalizando R$ 400 mil.

Os ingressos são vendidos à vista no valor de R$ 350 e tem início 1 mês antes do evento. O local pretendido para o evento tem capacidade máxima de 3000 pessoas. A expectativa é de casa lotada para o evento.

A partir das informações monte o diagrama de fluxo de caixa desse projeto
Determine qual demanda por ingresso será possível afirmar que o projeto não é interessante do ponto de vista financeiro.
Se a capacidade máxima do local for reduzida para 2500. A resposta o item anterior permanece a mesma?

Exercício Resolução

\[ \begin{align} VPL = &\underbrace{-100.000}_{t_0} +\underbrace{(-300.000 - h_1)}_{t_1} +\underbrace{(750.000 - h_2)}_{t_2} \\ & + \underbrace{(-100.000 - h_3)}_{t_3} + \underbrace{(-100.000 - h_4)}_{t_4} ,\,\,\ h_j \geq 0\\ = & -100.000 -300.000 - h_1 +750.000- h_2 \\ &-100.000 - h_3 -100.000 - h_4 \\ = & 150.000 - (h_1 + h_2 + h_3 + h_4) \\ \end{align} \] \[ \begin{align} 0 \leq VPL \Longleftrightarrow 0 & \leq 150.000 - h_T ,\,\,\ \text{onde } (h_{T} = h_1 + h_2 + h_3 + h_4)\\ \Rightarrow h_T & \leq 150.000 \\ \end{align} \]

Exercício Resolução

\[ \begin{align} VPL = &\underbrace{-100.000}_{t_0} +\underbrace{(-300.000 - h_1)}_{t_1} +\underbrace{(575.000 - h_2)}_{t_2} \\ & + \underbrace{(-100.000 - h_3)}_{t_3} + \underbrace{(-100.000 - h_4)}_{t_4},\,\,\ h_j \geq 0 \\ = & -100.000 -300.000 - h_1 +575.000- h_2 \\ &-100.000 - h_3 -100.000 - h_4 \\ = & -25.000 - (h_1 + h_2 + h_3 + h_4) \\ \end{align} \]

\[ \begin{align} 0 \leq VPL \Longleftrightarrow 0 & \leq -25.000 - h_T ,\,\,\ \text{onde } (h_{T} = h_1 + h_2 + h_3 + h_4 )\\ \Rightarrow h_T & \leq -25.000 \\ \end{align} \]

Diferença entre DRE e DFC

Concepção de Juros

Interpretação do Juros

Remuneração do capital empregado em atividade produtiva.
Custo de capital de terceiros.
Remuneração paga/cobrada por instituição financeira sobre o capital nela aplicado/tomado.
Pode ser visto como o valor do aluguel do dinheiro.

Unidade e Medida

Os juros são fixados por meio de taxas percentuais referente a uma determinada unidade de tempo.
O período referente a taxa pode ser ao dia (a.d.), ao mês (a.m.), ao semestre (a.s.), ao ano (a.a.) etc.

Objetivos Matemática Financeira

Realização de cálculo envolvendo fluxo de caixa, com a correta aplicação de taxa de juros, para se levar em conta o valor do dinheiro no tempo.
Obtenção da taxa interna de juros que está implícita nos fluxos de caixa.
Análise e comparação de diversas alternativas de projetos de investimentos.

Fundamentos

A abordagem da matemática financeira centra-se nos seguintes ‘axiomas’:

Sejam $V_{t}$ e $V'_{t}$ valores de algum ativo numa economia no tempo $t$. Se $V_{t}=V'_{t}$ então eles representam a mesma quantidade de recurso. Isto é, valores para uma mesma data são grandezas que podem ser operadas algebricamente sem perda da referência de valor.
Seja $t>0$ e $V_{t}=V'_{0}$ então ambos os ativos não possuem a mesma quantidade de recurso. Em outras palavras, as quantidades de recursos representadas em datas diferentes não podem ser comparadas diretamente.

Valor de um Ativo no Tempo

Para podermos comparar dois ativos quaisquer, $V_{t_{1}}$ e $V'_{t_{2}}$, precisamos de um mesmo referencial no tempo. Se for conhecido a função que descreve a evolução de um dos ativos, então basta ajusta-lo para uma data em comum.

\[ \begin{align} V_{t}& = \psi_{a}(t,V_{0}) \\ \end{align} \]

Caso $V'_{t_{2}}>\psi_{a}(t_{2},V_{0})$ então $V'_{t_{2}}$ representa uma maior quantidade de recurso do que $V_{t_{2}}$. Logo, $\psi_{a}(t,V_0)$ descreve a evolução do ativo $V_t$ ao longo do tempo.

Exemplo: Valor de um Ativo no Tempo

Capitalização Contínua

Considere um caso bem simples de capitalização de um ativo $V_{t}$. Esse ativo remunera de forma proporcinal ao montante aplicado. Além disso, considere uma aplicação inicial $m_{0}$ em $t=0$. Desta forma, temos

\[ \begin{align} \frac{d}{dt}V_{t} \propto V_{t} & \Rightarrow \frac{d}{dt}V_{t} = aV_{t} \\ \frac{d}{dt}\log V_{t}& = a\,\,\,\ a\in\mathbb{R}\\ \log V_{t} - \log m_{0}& = at+C \,\,\,\ (C=0 \text{ pelo } PVI)\\ V_{t} = m_{0}e^{at} & \Rightarrow \psi_{a}(t,m_{0})= m_{0}e^{at} \end{align} \]

Gráficos: Valor e Remuneração

Capitalização Contínua

Podemos ainda considerar a capitalização de um ativo $V_{t}$ com valor inicial $m_{0}$, no qual sua capitalização é proporcional ao montante investido inicialmente.

\[ \begin{align} \frac{d}{dt}V_{t} \propto m_{0} & \Rightarrow \frac{d}{dt}V_{t} = m_{0}\cdot a \\ \frac{d}{dt}V_{t}& = m_{0} \cdot a\\ V_{t} & = m_{0}\cdot a \cdot t + m_{0}\\ & = m_{0}(1+at) \end{align} \]

Gráficos: Valor e Remuneração

Classificação Regimes e Séries

Por referência de capitalização
1. Juros Simples
2. Juros Compostos
Por período de capitalização
1. Contínuo
2. Discreto

Por regularidade
1. Séries Regulares
2. Séries Irregulares
Por risco
1. Séries Certas ou Determinísticas
2. Séries Aleatórias ou Estocásticas
Por tempo
1. Série Finita
2. Série Infinita

Moeda

Ativo financeiro de aceitação geral utilizado na troca de bens e serviços que tem o poder liberatório (capacidade de pagamento) instantânea. Sua aceitação é garantida por lei. Ela tem curso “forçado” e sua única garantia é a legal.

Função da moeda numa economia

Meio ou instrumento de troca
Unidade de medida ou unidade de conta
Reserva de valor

Moeda e Inflação

A moeda representa um direito sobre as mercadorias de uma economia. Ela pode ser guardada para uso posterior, visto que serve como reserva de valor ou forma de poupança. Note que a moeda serve de reserva de valor para um determinado agente, mas não para toda a sociedade. O que determina a riqueza de uma economia é a sua capacidade de produção global e não o montante de moeda existente.

Inflação

Inicialmente vamos considerar a hipótese de uma moeda estável. Posteriormente vamos trabalhar com o caso de moedas não estáveis. Os conceitos da matemática financeira são integralmente aplicáveis em ambos os casos.